ヘリウムを使わずにヘリウム風船を復活させることはできるのか！？前代未聞の思考実験！！

黒豆：ディズニーランドに行ってからかれこれ1ヶ月経つけど、本当に楽しかったよね～！

のた：そうだね。たまにはプチ贅沢してディズニーランドもいいよね。

黒豆：本当にね～。思わず風船も買っちゃったし！！あの風船、1ヶ月経つけどまだかろうじて浮いてるね。

黒豆：ああ、でももうちょっとで地面についちゃいそう・・・。ああ～、なんだかディズニーランドの思い出が消えるみたいで寂しいなあ・・・。この風船、また上昇させることはできないのかなぁ。

のた：じゃあ、どうやったら風船が復活するか考えてみようか！

黒豆：えっ？えーと、あ、そうか！ヘリウムを入れればいいんだ！簡単じゃん！！

のた：それじゃあ面白くないじゃん。ヘリウムを入れなくても、一時的にヘリウム風船を上昇させることができないか考えるんだよ。

黒豆：えっ！！そんなことできるのかなぁ？？

のた：分からないけど、考えてみると面白いと思うよ。ちなみに、こんな風に頭の中だけで想像するだけの実験のことを「思考実験」と言うんだ。

さぁ、楽しい楽しい思考実験の始まりだ！！

ヘリウム風船が浮く原理

のた：まず前提として、ヘリウム風船が浮く原理について確認しておこう。ヘリウム風船がなぜ浮くかは知ってる？

黒豆：えーっと、ヘリウム風船に浮力が働くからだよね。確かヘリウムガスは空気より密度が小さいから・・・えーと・・・（ごにょごにょ）。

のた：・・・そうだね。一応順に説明しよう。

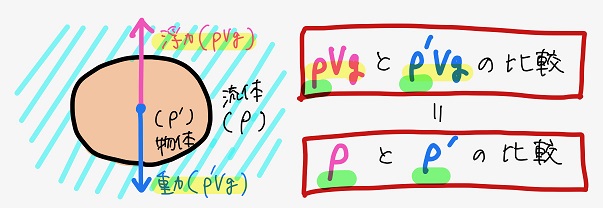
まず、浮力の定義からだ。浮力の定義は

浮力の定義

\(f=ρVg\)

\(f\)：浮力[\(N\)]
\(ρ\)：流体の密度[\(kg/m^3\)]
\(V\): 浮力が及ぼされる物体の体積[\(m^3\)]

だね。

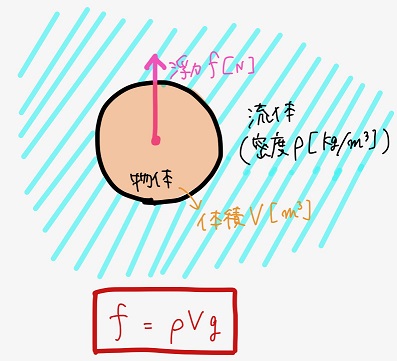
この定義は「物体に働く浮力の大きさは物体が排除した流体の質量に等しい」ということを表していて、「アルキメデスの原理」としても知られている。

当然だけど物体には浮力の他に重力も働く。そして、

流体中の物体が浮くかどうかは、その物体に働く浮力と重力との関係で決まる。

物体に働く浮力が重力より大きければ物体は浮くし、逆なら沈むんだ。

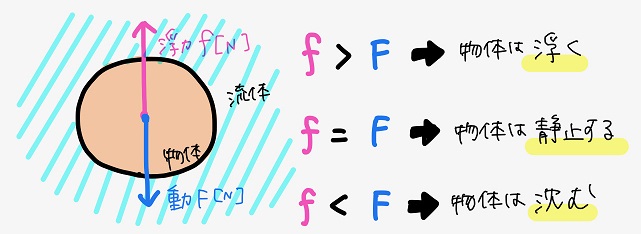
さらに、物体の密度をρ’とすると物体に働く重力はρ’Vgで表すことができるから、

浮力であるρVgと重力であるρ’Vgの比較は、流体の密度ρと物体の密度ρ’との比較と等価になるんだったね。

つまり、

物体と流体の密度を比較するだけで物体が浮くか沈むかが分かるんだ。

このことから考えると、

ヘリウムガスの密度は空気の密度よりも小さいんだから、ヘリウム風船は空気中で浮く

ってことが分かるよね。

「温度」と「密度」との関係に着目してみよう

のた：物体が浮くかどうかは、物体と流体の密度差と関係があるってことが分かったね。

今回の場合、物体はヘリウム風船で、流体は部屋の空気だ。

つまり、

ヘリウム風船内のヘリウムガスの密度と部屋の空気の密度をそれぞれ変化させることで、浮力を重力よりも大きくして風船を浮かせることができる可能性があるね。

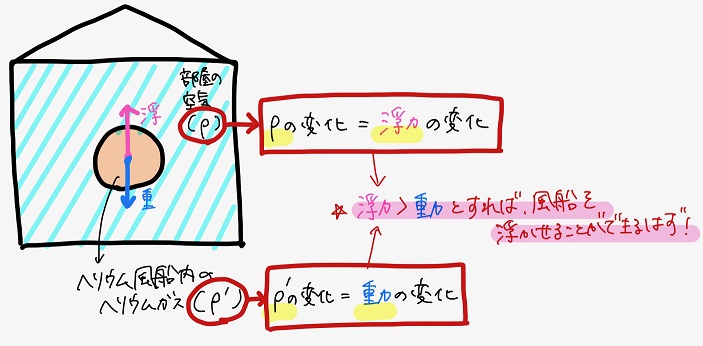
密度を変化させる簡単な方法、何だか分かる？

黒豆：ええとお・・・。温度を変化させる？？

のた：ご名答！そうだね。エアコンなどで部屋の温度を変化させることで気体の密度を変化させることができるね。

じゃあ、部屋の温度を変化させると気体の密度がどう変化して、その結果浮力や重力がどう変化するのか考えてみよう！

思考実験：室温を変化させるとヘリウム風船は復活するのか

気体の「温度」と「密度」との関係は？

のた：まずは、気体の温度と密度との関係を知る必要があるよね。

黒豆：おっ、もしかして！理想気体の状態方程式を使うんじゃない？？

のた：ご名答！理想気体の状態方程式を使って、温度と密度との関係を考察するんだ。

この状態方程式は理想気体で成立するものだから実在の気体とは少しズレがあるけど、今回はそこは無視しよう。

黒豆：理想気体の状態方程式って、確かこうだよね。

理想気体の状態方程式

\(PV=nRT\)

\(P\)：圧力[\(Pa\)]
\(V\)：体積[\(m^3\)]
\(n\)：物質量[\(mol\)]
\(R\)：気体定数（8.314[\(J/K・mol\)]）
\(T\)：温度[\(K\)]

のた：そうだね。で、この気体の方程式を変形して温度と密度との関係式を導出してみよう。

気体の状態方程式の変形

最初の式は、
\(PV=nRT\)

分子量\(M\)[\(kg/mol\)]と質量\(w\)[\(kg\)]を用いて書き換えると、

\(PV=(w/M)RT\)
\(P=(w/V)(RT/M)\)

ここで、密度\(ρ\)[\(kg/m^3\)] = \(w/V\)だから、

\(P=ρRT/M\)
\(P(M/R)=ρT\)

\(R\)と\(M\)は定数なので、別の定数\(k\)を用いて\(k=M/R\)とすると、

\(kP=ρT\)

となる。

のた：\(ρ\)と\(T\)が入った、\(kP=ρT\)という式が出てきたね。さて、この式を使って温度\(T\)と密度\(ρ\)との関係を考えてみよう。

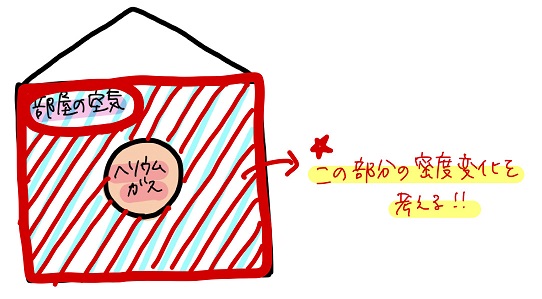
密度変化を考える対象は2つ。

「部屋の空気」と「ヘリウム風船内部のヘリウムガス」だ！

これらの密度がどう変化するかを考えてこれらの密度差を求めることで、風船が浮くかどうかが分かるよね。

じゃあ、順に考えてみよう。

①部屋の空気の密度変化

のた：まずは「部屋の空気」の密度変化からだ。さっき状態方程式から導出した式

\(kP=ρT\)

を使って考えていこう！

この式から温度\(T\)と密度\(ρ\)との関係を考えればいいんだけど、式中には圧力\(P\)という変数もあるよね。こうなると変数が3つになるから、\(T\)と\(ρ\)との関係を考えるのが難しくなる。どうすればいいかな？？

黒豆：うーん、圧力\(P\)を変数じゃなくて定数と考えることができればいいってことだよね。今回の場合、圧力\(P\)を定数と考えることはできるのかなぁ。

のた：じゃあ、圧力\(P\)に関する条件を考えてみよう。

部屋というものは完全に密閉されていることはあり得ない。ぜったいどこかに隙間があって、空気が出入りしているはずだよね。

空気が出入りしているってことは、部屋の圧力は常に一定であると考えられるって考えられない？？

黒豆：あ！確かに！！

のた：そこで今回は、さっき黒豆が言ってたように\(P\)=一定であると仮定しよう。

すると上の式は、新たな定数\(m\)を導入して

\(ρT = m\)

とすることができる。

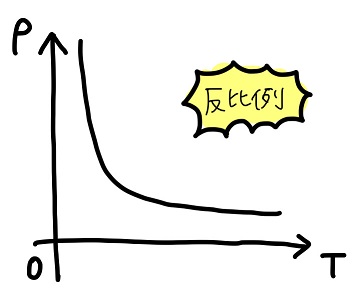
これはつまり、

今回考える条件の下では部屋の空気の密度\(ρ\)と温度\(T\)は反比例する

と言えるってことだ！

黒豆：おお！なるほど～！！状態方程式から始まって、大分すっきりしてきたね。

のた：そうでしょ。いくつか仮定を置くことで思考実験がしやすくなるんだよ。

部屋の空気の密度\(ρ\)と温度\(T\)が反比例するってことは、まとめるとこういうことだね。

部屋の空気の密度変化

温度\(T\)：高　→　密度\(ρ\)：小　→　風船に働く浮力：小
温度\(T\)：低　→　密度\(ρ\)：大　→　風船に働く浮力：大

②ヘリウム風船内部のヘリウムガスの密度変化

のた：さあ、次は風船内部のヘリウムガスの密度変化について考えてみよう。

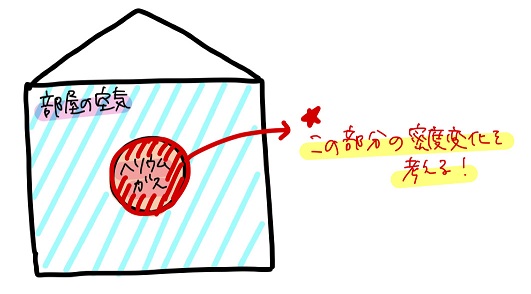
部屋の空気の場合と同じく、以下の式から始めるよ。

\(k’P’=ρ’T’\)

（※部屋の空気の場合と区別するため、各変数および定数にはプライムを付ける）

黒豆：今回も部屋の空気の場合みたいに、圧力\(P\)の条件を考える必要があるよね。

のた：そうだね。言ってしまうと、仮定によってはヘリウムガスの場合も圧力\(P\)=一定と考えることができるんだ！

黒豆：えっ、何で？？

のた：ここはちょっと分かりにくいかもしれないんだけど・・・。風船の微小部分に働く力を考えてみると分かるよ。

風船の微小部分に働く力には外圧、内圧、張力の3つがあって、これらが以下のように釣り合っているんだ。

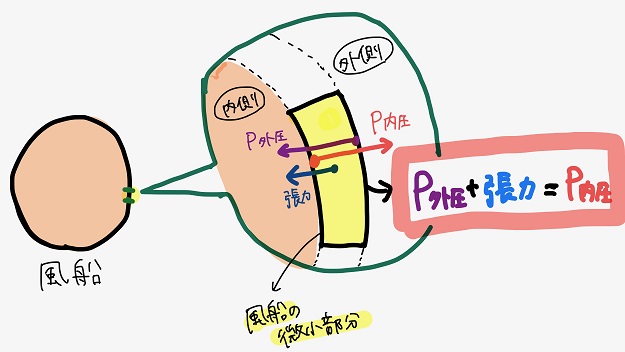
上図中の関係式、

\(P_{外圧} + 張力 = P_{内圧}\)

は平衡状態では常に成立する式だ。初期条件がどうであれ、最終的にはこの式が成立するようになるってことだね。

で、張力の大きさは風船の材質によって異なるんだけど、今回は簡単化のために\(P_{外圧}\)や\(P_{内圧}\)に比べて張力は無視できるほど小さいと仮定しよう。ビニール風船みたいなイメージかな。

つまり上の式は、

\(P_{外圧} = P_{内圧}\)

と近似できる。

で、今回の\(P_{外圧}\)は部屋の空気の圧力\(P\)で、それは一定であると既に仮定してるんだから・・・？

黒豆：\(P_{内圧}\)、つまりヘリウム風船内のヘリウムガスの圧力\(P’\)も一定だと仮定してよい、ってことなんだね！

のた：その通り！！

黒豆：なんかなんとなくだまされたような気がしてすっきりしないけど・・・。

のた：うーん、まあぱっとイメージはしづらいかもね。この部分に関しては機会があればより詳しく説明しよう。

とりあえず、ヘリウムガスの圧力\(P’\)も一定だと考えることができるんだから、部屋の空気の場合と同じように以下の反比例の関係式が成立するよね。

\(ρ’T’ = m’\)

てことは、まとめると以下のようになる。密度\(ρ’\)と温度\(T’\)の間の関係は部屋の空気の場合と同じだね。

ヘリウム風船内部のヘリウムガスの密度変化

温度\(T’\)：高　→　密度\(ρ’\)：小　→　風船に働く重力：小
温度\(T’\)：低　→　密度\(ρ’\)：大　→　風船に働く重力：大

では、部屋の温度をどうすれば風船は浮くのか？？

のた：これまでの考察結果をもう一度確認してみよう。

部屋の空気の密度変化

温度\(T\)：高　→　密度\(ρ\)：小　→　風船に働く浮力：小
温度\(T\)：低　→　密度\(ρ\)：大　→　風船に働く浮力：大

ヘリウム風船内部のヘリウムガスの密度変化

温度\(T’\)：高　→　密度\(ρ’\)：小　→　風船に働く重力：小
温度\(T’\)：低　→　密度\(ρ’\)：大　→　風船に働く重力：大

のた：最初は\(ρ = ρ’\)、つまり風船に働く浮力と重力が等しいと仮定して、そこから温度変化により\(ρ\)と\(ρ’\)がどう変化する可能性があるかを図解してみよう。とりあえず、温度を高くした場合について考えてみた。

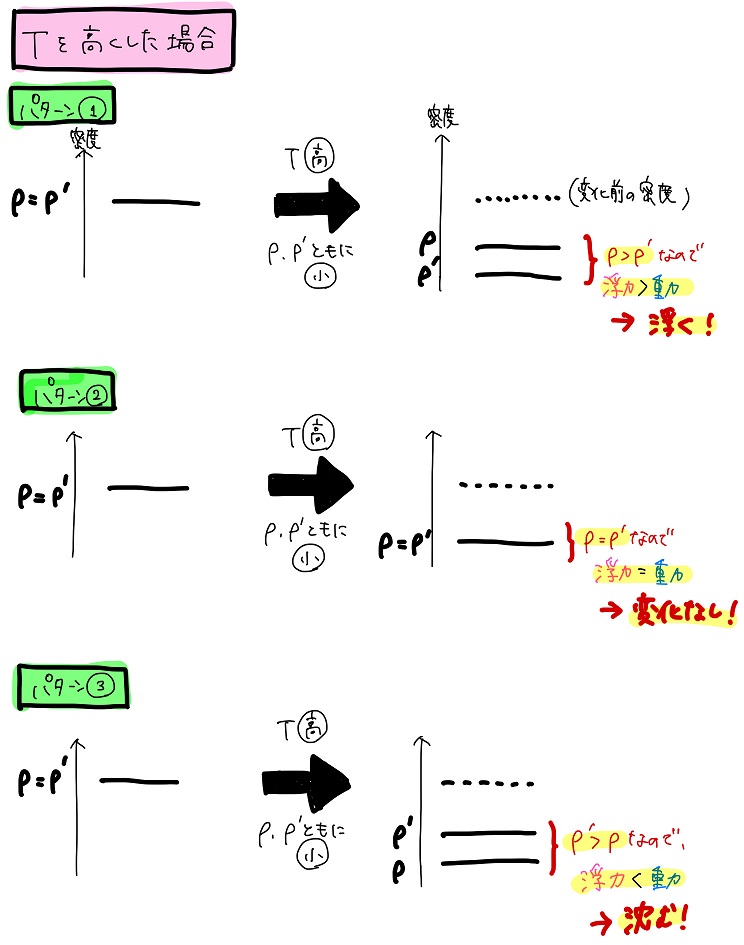
のた：こんな感じかな。浮く場合、変化しない場合、沈む場合の3つのパターンがある。温度を低くした場合も同じく3つのパターンが考えられるね。

黒豆：うーん、温度を高くしても低くしても\(ρ\)と\(ρ’\)の変化方向は同じだから、ρとρ’の変化の大きさによって浮くか沈むかが決まるってことだね。

つまり、温度を高くしても低くしても、浮く可能性も沈む可能性もあるってことだよね。なんかここにきて、結局答えになってない気が・・・。

のた：そうみたいだね・・・。こうなると、実際に\(ρ\)と\(ρ’\)を計算しないと難しそうだなあ。

さっき状態方程式から導出した以下の式

\(kP=ρT\)

\(k’P’=ρ’T’\)

を使ってある2つの温度での部屋の空気とヘリウムガスの密度を計算して、空気とヘリウムガスのうち、温度による密度変化が大きいのはどっちかを考えてみよう。

まずは空気とヘリウムガスに関して\(k\)と\(k’\)を求めて、\(P\)と\(P’\)はどちらも一定だから1と置いて、\(300K\)(27℃)と\(290K\)(17℃)での\(ρ\)と\(ρ’\)の値を計算すると・・・、ごにょごにょ・・・。

黒豆：（うおぉ、すごく集中してる・・・！邪魔しないでおこう・・・）

のた：できた！

空気に関する計算結果

【有効数字2桁で計算した場合】
\(300K\)(27℃)：\(ρ\) = \(1.6×10^{-6}\)[\(kg/m^3\)]
\(290K\)(17℃)：\(ρ\) = \(1.7×10^{-6}\)[\(kg/m^3\)]
密度変化：\(0.1×10^{-6}\)[\(kg/m^3\)]

【有効数字3桁で計算した場合】
\(300K\)(27℃)：\(ρ\) = \(1.60×10^{-6}\)[\(kg/m^3\)]
\(290K\)(17℃)：\(ρ\) = \(1.66×10^{-6}\)[\(kg/m^3\)]
密度変化：\(0.06×10^{-6}\)[\(kg/m^3\)]

ヘリウムガスに関する計算結果

【有効数字2桁で計算した場合】
\(300K\)(27℃)：\(ρ’\) = \(1.2×10^{-5}\)[\(kg/m^3\)]
\(290K\)(17℃)：\(ρ’\) = \(1.2×10^{-5}\)[\(kg/m^3\)]
密度変化：0[\(kg/m^3\)]

【有効数字3桁で計算した場合】
\(300K\)(27℃)：\(ρ’\) = \(1.16×10^{-5}\)[\(kg/m^3\)]
\(290K\)(17℃)：\(ρ’\) = \(1.20×10^{-5}\)[\(kg/m^3\)]
密度変化：\(0.04×10^{-5}\)[\(kg/m^3\)]

のた：うーーーん、有効数字2桁の結果を比較すると空気の方が温度による密度変化が大きいけど、有効数字3桁の結果だとヘリウムガスの方が密度変化が大きい・・・これは・・・！！

黒豆：これは・・・？？？？

のた：どっちも同じくらい、ってことだね。

黒豆：ずこーーーっ！！

え？てことは、空気とヘリウムでは温度による密度変化は同じくらいってことだから、

温度を高くしても低くしても風船は浮きも沈みもしないってこと？？

のた：そうなっちゃうね～。さっき考えたパターン②だね。