~家具屋さんにハイテーブルを買いに来た「のた」と「黒豆」~
黒豆:わー!ハイテーブルがたくさんあるね!!どれにするか迷っちゃうな~。
のた:こらこら、そんなに走ると危ないよ・・・
黒豆:あ、これ見て!!机の脚が外側に向いててなんだかオシャレじゃない??
のた:へぇー、こんな机も売ってるんだねぇ。でも、何だかハイカラ過ぎて僕には似合わない気が・・・
黒豆:そう??じゃあやっぱり一般的な形のがいいかなぁ。これはどう?
のた:うん、こんな形でいいかな・・・。普通が一番・・・。
黒豆:それにしても、同じ四角形の面を持つ机でも、脚の形にはいろんなバリエーションがあるんだね~。
黒豆:机って安定してることが一番重要だと思うんだけど、どの机が一番安定してるんだろうね??
のた:ふむ。面白い質問だね。じゃあ、ちょっと考えてみようか!
「安定」「不安定」とは何かを定義しておこう
のた:どの机が一番安定しているのか。これを考えるには、まず
「安定」「不安定」とは何か?
を定義しておく必要があるね。
黒豆:そっか。確かにこれを定義しないと議論できないよね。
のた:その通り。
じゃあ黒豆、「不安定」な机ってどんなだと思う?
黒豆:うーん、倒れやすい机かなぁ。上に物を置いたときにぐらぐらしたり、倒れたりするような。
のた:オーケー。じゃあ今回は、
机の安定性 = 「上に物を載せたときの倒れにくさ」
と定義して話を進めよう。

物はどんなときに「倒れる」のか??
のた:机について考える前に、まずは物が「倒れる」という現象について考えてみよう。
物が「倒れる」ときって、一体何がおこってるか分かる??
黒豆:ええ~と・・・。全体のバランスが崩れてそうだけど・・・。
のた:まあそれはそうなんだけど、もっと物理っぽく考えてみようか。
以下の2つの物体を考えよう。どっちの物体も床の上に置いてあるだけの状態だ。床に固定してはいない。
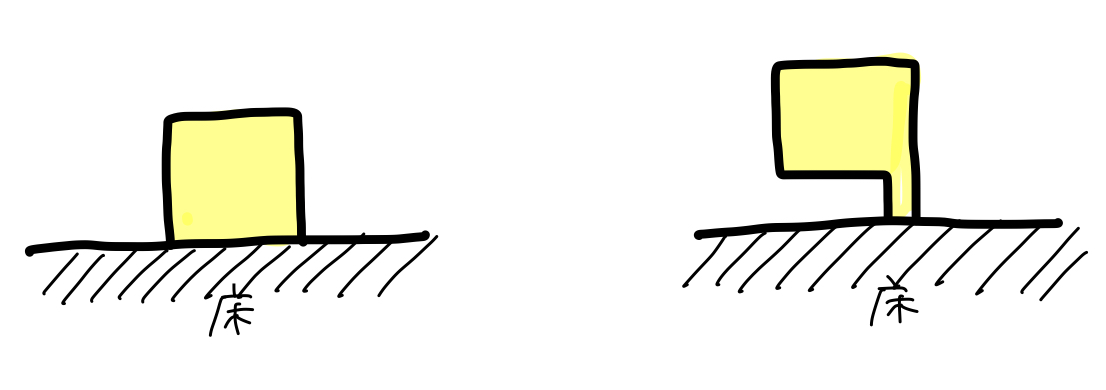
この2つの物体、どっちもこのまま倒れずに安定してると思う?
黒豆:うーんと、右側の物体はバランスが悪くて倒れそうだけど・・・。
のた:バランスが悪いって、どういうことかな?何で倒れそうなんだろう??
黒豆:ええと・・・汗。ちょ、直感的に・・・・。
のた:ここでキモになるのは、「重心」だよ。重心って何か覚えてる?
黒豆:確か・・・、
物体の各部分に働く重力を合成した合力の作用点。重心を支えると物体全体を支えることができる。
だよね。
のた:そうだね。つまり、物体を安定して支えるには重心を支える必要があるんだ。
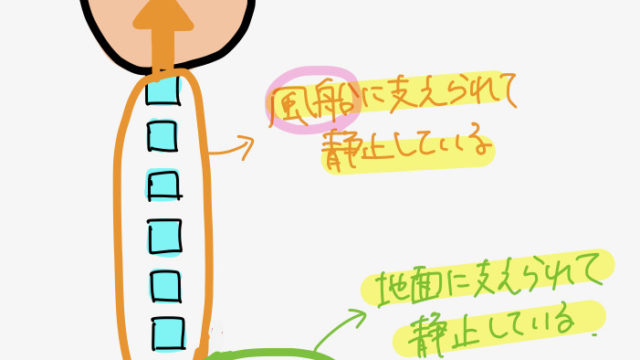
例えば下の図では、物体の重心が物体内部にあって、手は物体よりも大きい。
つまり物体の重心の下には手がある状態だから、手からの垂直抗力で物体を支えることができるんだ。
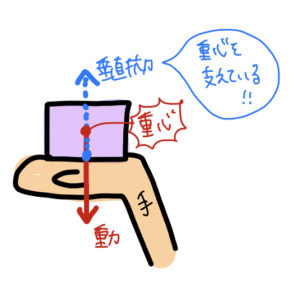
黒豆:あっ。てことは・・・!
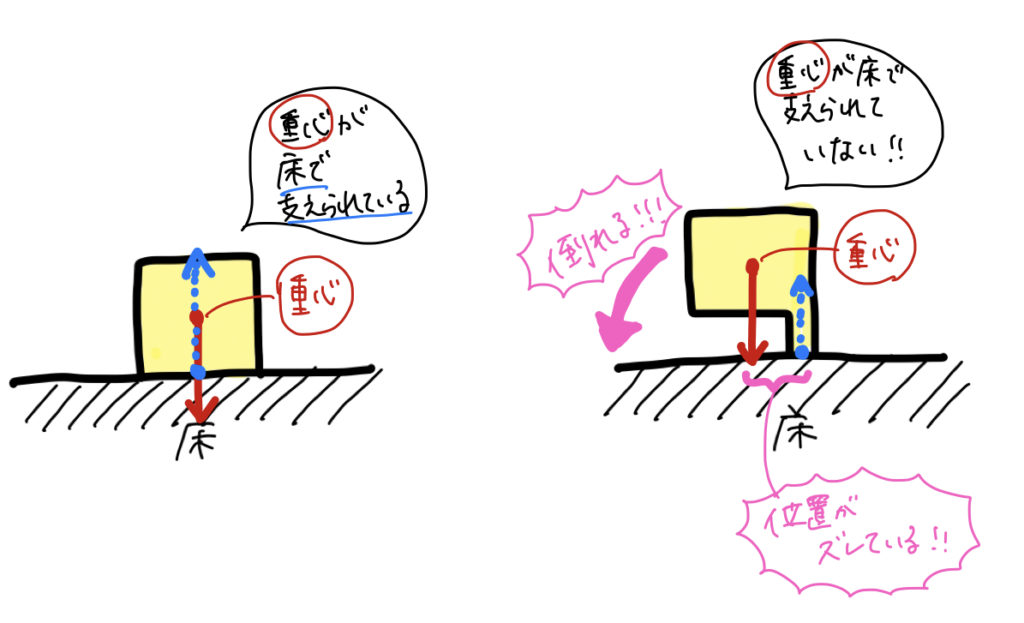
のた:気付いたかな?つまりさっきの図の場合、
左側の物体の重心は物体が床と接している領域にあるけど、右側の物体の重心は床と接していない領域にある。
つまり、右側の物体では重心が床で支えられていない(重心位置と床からの垂直抗力の位置がズレている)ので物体が倒れてしまう
んだ!!
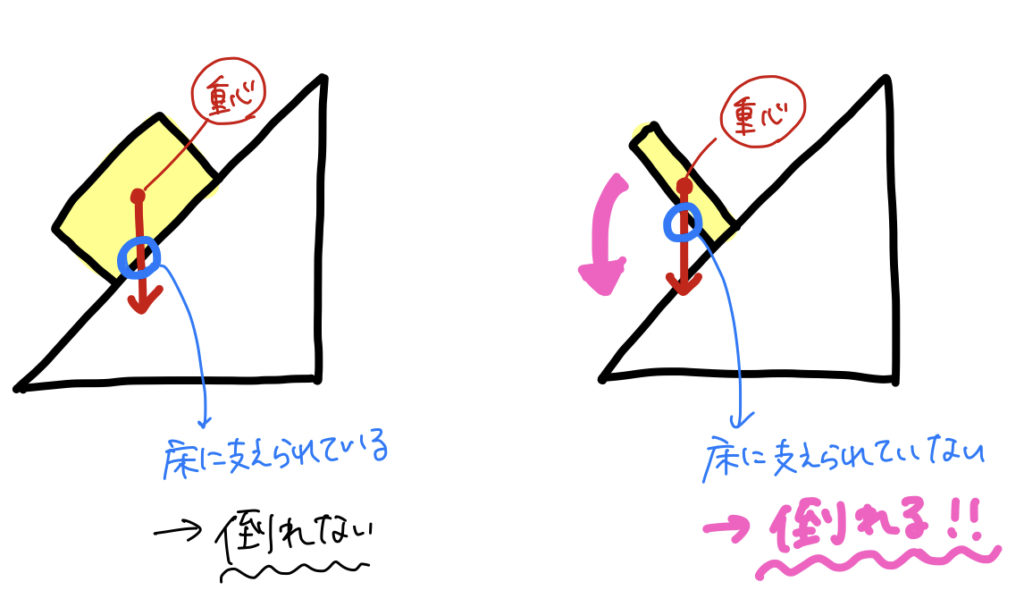
斜面に物体を置く場合にも同じようなことが言えるよ。
机の安定性について検討しよう
のた:じゃあ、机の話に戻ろう。
机の上に何か物を載せたとする。すると、どういう条件のときに机は倒れるのかな?
黒豆:えーと、さっきと同じように、
重心を支えることができているかどうか
を考えればいいんだよね。
この場合、机に物体を載せたんだから、支える対象は「机+物体」全体の重心になるのかなぁ。

のた:そうそう、鋭いね。じゃあ、その重心を支えるのはどこ?
黒豆:さっきの例と同じように考えたら床のはずだよね。あれ?でも、床と接してるのは机の脚部分だけだから・・・。
机の脚に働く垂直抗力が重心を支えるのかな??
のた:そうそう、その通り!
「机+物体」の重心を支える位置(重心と同一線上)に、床からの垂直抗力が働けばいいんだよ。
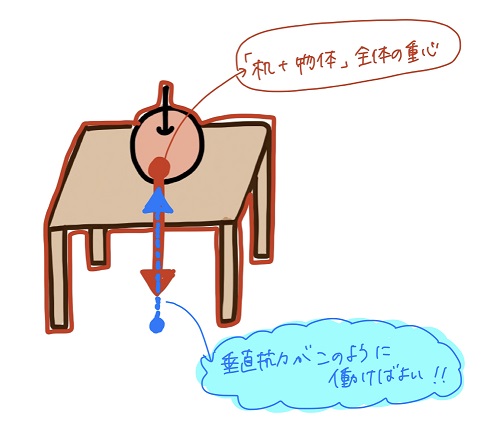
黒豆:でもさ、机の脚が4本だとしたら、その4本全てに床からの垂直抗力が働くよね・・・。
この垂直抗力、どれも「机+物体」の重心からはズレてて、とても重心を支えてるようには思えないんだけど??
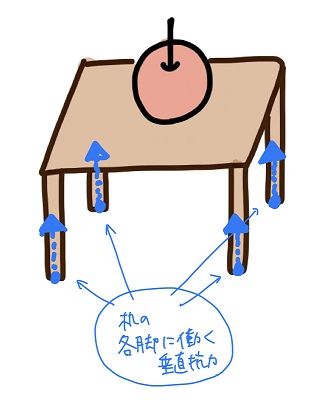
のた:このケースでは、垂直抗力の「合力」を考えるんだよ。
平行な2つのベクトルは合成して1つのベクトルにできるんだ。
このとき、元のベクトルが同方向であれば、合成されたベクトルは必ず元のベクトルの間に存在する。
(こちらのサイトが分かりやすいよ!)
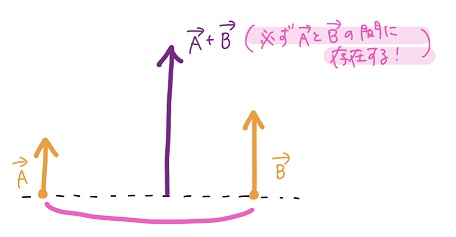
黒豆:てことは・・・、2本の脚に働く垂直抗力の合力は必ず2本の脚の間に存在するってことだね!!
のた:そうだね。
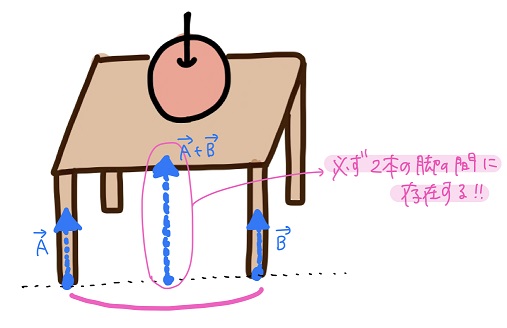
そして机の脚が4本の場合、垂直抗力を順に合成していくと、4つの垂直抗力の合力は必ず4本の脚を結んだ線の内側領域に存在するんだ!
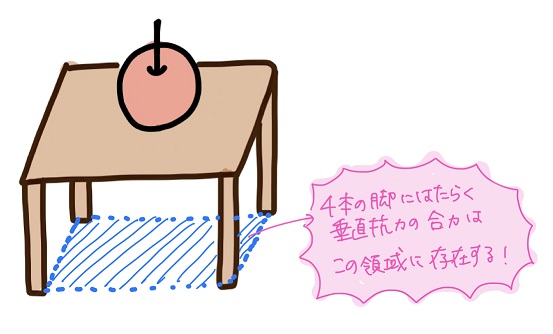
黒豆:おお!じゃあ、
「机+物体」の重心がこの領域にある場合には、床からの垂直抗力の合力によってその重心を支えることができる
ってことだね!
のた:その通り!まとめると、
「机+物体」全体の重心が机の脚を結んだ線の
内側領域にある→机は倒れない。
外側領域にある→机は倒れる。
ってことだね!
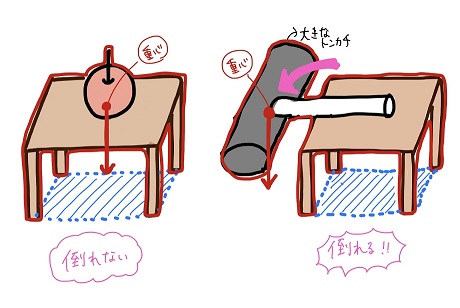
黒豆:なるほど~!!!重心が直接床に支えられてなくても、床からの垂直抗力の合力が重心を支えると考えればいいんだね。
より安定した机、とは??
黒豆:ほうほう。わかってきたぞ~!てことは、
机の脚を結んだ線の内側領域が広いほど、机の安定性は大きいんだね。
「机+物体」の重心が存在できる範囲がそれだけ広いってことだから。
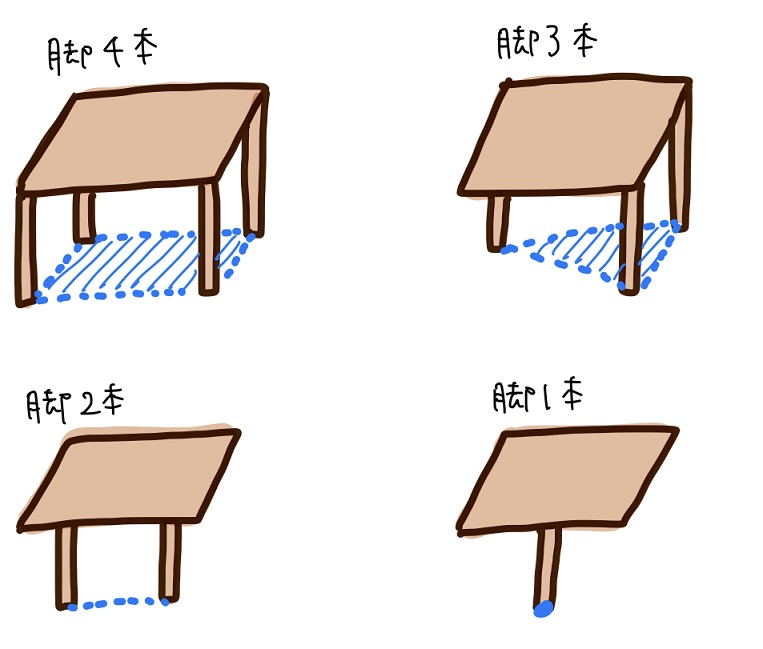
のた:そうだね。例えば、脚の本数により内側領域の広さがどうなるか見てみようか。
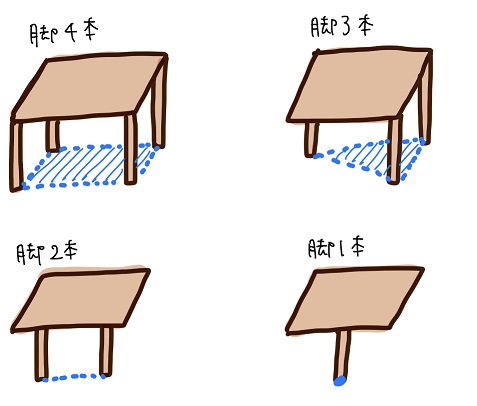
黒豆:4本脚だと内側領域が一番広いから一番安定だね。
脚の本数が減るにつれて段々内側領域が狭くなって・・・。
1本脚だと、脚の真上に物体を置かない限り机は倒れちゃう。
のた:そだね。じゃあ、4本脚の机をさらに安定させたいときはどうすればいいと思う??
黒豆:えっ??えっと・・・、脚の内側領域の面積を大きくすればいいんだよね・・。
でも、これ以上大きくなるかなぁ?
のた:こうすればどう??
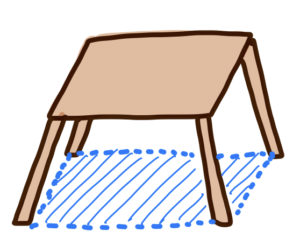
黒豆:あっ!なるほど!!
こうやって脚を外側に向ければ、それだけ内側領域が広くなるね!広くなった分だけ安定しそう!!
のた:そうでしょ。例えば、産まれたばかりの子鹿は足を外側に向けて立つんだよ。
その方が普通に立つより安定するからね。

黒豆:本当だ~!かわいいなぁ・・。
発展:変わった脚をもつ机の場合は?
黒豆:思ったんだけどさ、例えばT字の脚をもつこんな机の場合は・・・、
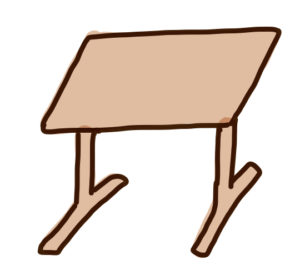
以下の青い領域に重心があればいいってことになるんだよね?
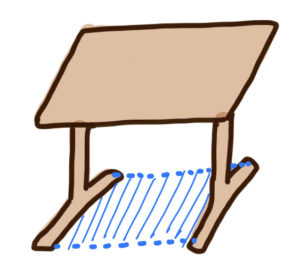
のた:そう!よく気がついたね~!!
T字脚の床と接している部分に働く垂直抗力の合力は、青い領域に存在することになるね。
つまり、T字脚2本で普通の脚4本と同じ四角い領域の重心をカバーできる、ってことになる。
もちろん、強度とか別の問題はいろいろあると思うけど、今回議論している「安定性」に関して言えば両者は同じだね。
まとめ
黒豆:今日の話は面白かったな~!テーブルを見る目が変わるよね。
のた:身近にあるものがどうしてその形をしているのか、ということを考えると楽しいよね。
その形であることには必ず理由があるはずだからね。
黒豆:そうだね~!さぁて、じゃあ疲れたし帰ろっか!!
のた:いや、ハイテーブルを買いに来たんだけど・・・汗
・・・まあ、また次回でいっか・・・。