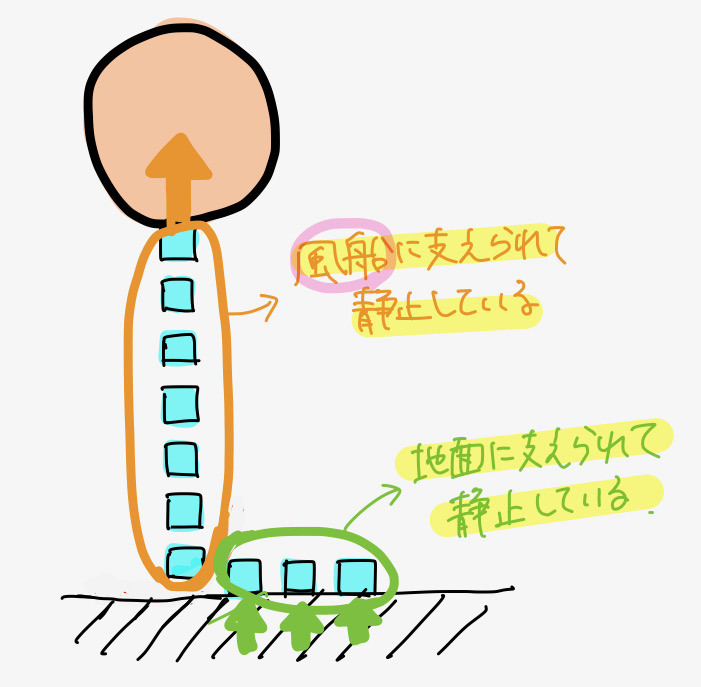
黒豆:この前ヘリウム風船を復活させられるかどうかについて考えたけど・・・。結局部屋の温度を変化させるだけじゃ風船を復活させることはできないって結果になったよね。
せっかく風船をまた浮かせることができるかと思ったのに~。残念だったなぁ・・・。
↓ヘリウム風船の復活方法に関する記事はこちら!!↓

のた:まあまあ、あれは仮定をたくさん置いた思考実験だからね。実際にやってみると復活するかもしれないよ。
黒豆:うーん、まあそうだけどさぁ。
そういえばあの後少し気になってたことがあるんだけど。
ヘリウム風船って、実際はこんな風にヒモがついてるよね。

でも確か前回は、風船にはヒモが付いてないと仮定してこんな風に考えたよね。
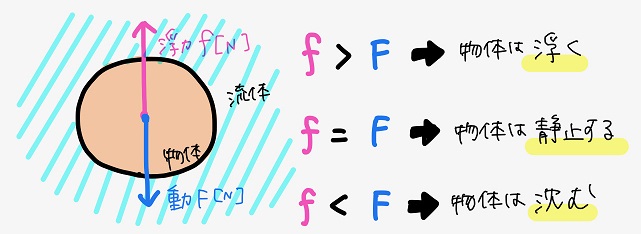
ヒモが付いてると風船が復活したりしないのかなぁ?
のた:うーん、ヒモが付いてると風船が浮いたり沈んだりするときの挙動は多少変化するけど、温度変化でヒモの密度が変化する訳ではないし、ヒモの有無が風船の復活如何に関係することはないと思うよ。
黒豆:そっかぁ、残念・・・。
のた:まあまあ。じゃあせっかくだから、
「風船にヒモが付いている場合に考えられる面白い状況」
について検討してみようか!
実は、風船にヒモが付いている場合にだけ考えることができる面白い状況があるんだよ~。この状況について考えてみると、ヒモ付きの風船を見る視点が変わるかも!
黒豆:へえ~、そうなんだ!やろうやろう!面白いこと大好き!!
ヒモが一部だけ地面についている状況について考えよう!
のた:ヒモ付き風船の面白い状況っていうのはこれだ!!
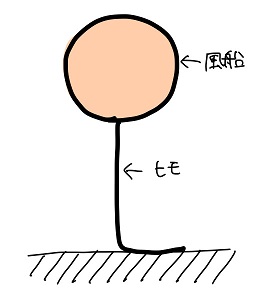
黒豆:えっ?これって、普通に風船が浮いてるだけだよね・・・。これのどこが面白い状況なわけ?
のた:よく見てみて。
ヒモの一部が地面についた状態で風船が静止している
でしょ。
これはヒモが付いている風船でだけ見られる特別な状況なんだよ。
黒豆:うーん、まあヒモが付いてなかったらそりゃこんな風にヒモを地面につけて静止はしないだろうけどさぁ。
それってヒモがないんだから当たり前じゃないの??この状況がそんなに面白いものだとは思えないんだけど・・・。
のた:ふふふ。まあまあ。この状況の本当の面白さはここからだよ。
問題提起:ヒモの浮いている部分と地面についている部分は同じように考えてよいのか?
のた:さて、ここからが面白いところだよ。
今回の状況では、ヒモ付きの風船のヒモの一部が地面についた状態で風船が静止しているよね。
この状況で、
系内で力がどのようにつり合っているのか
を考えてみよう。

この際、当然だけど「風船」と「ヒモ」の両方に働く力を検討しないといけないよね。
つまり、風船の他にヒモに働く重力や浮力についても考察する必要がある。
黒豆:うん、そりゃそうだよね。「風船+ヒモ」全体での力のつり合いを考える必要があるんだもの。
のた:そうだね。で、この力のつり合いを考える場合だけど、
空中に浮いているヒモと地面についているヒモに働く力は同じように考えてよいと思う?

黒豆:えっ!?うーん、よくない気がするけど・・・。
だって、地面についてる部分は地面から垂直抗力を受けてるはずだよね?対して空中部分は垂直抗力を受けてないはずだから、違う扱いにしないとだめだと思うなぁ・・・。
のた:うん、その通り!このような場合、
ヒモの空中に浮いている部分と地面についている部分に働く力は別々に考えないといけない
んだ。
これらに働く力は異なる、ってことだね。
じゃあ、今回の系ではヒモの各部分には一体どんな力が働いているのかを検討してみよう!
黒豆:おー!!(でも、別々に考えるだなんて一体どうやるんだろう・・・??)
ヒモの各部分に働く力を検討しよう!
検討するための条件を設定する
のた:今回は簡単化のために、以下の図のようにヒモを「手で」支えるとして考えよう。
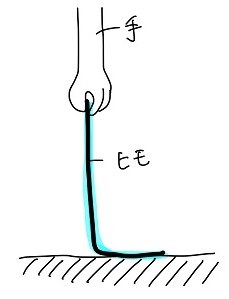
実際の系では手の変わりに風船がついてるけど、今はヒモにだけ注目したいからあえて風船を外してみた。
ちなみに、手がヒモに及ぼす力は風船の「浮力-重力」に相当するよ。
さて、このときヒモの空中に浮いている部分と地面についている部分にはそれぞれどんな力が働くのかを考える。
ところで、このようにある物の各部分について議論する場合には、
その物を微小部分に分割して考える
のが分かりやすいよ。
今回の場合、以下のようにヒモを微小部分に分割して考えてみよう。
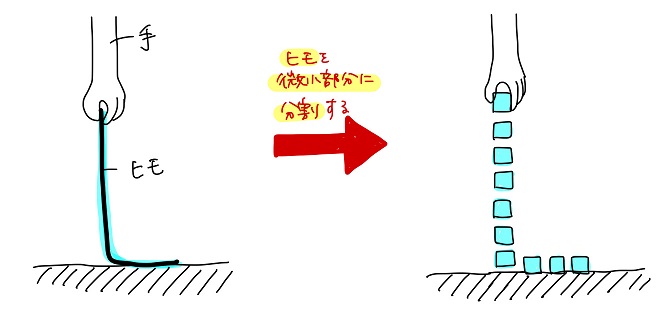
黒豆:おお!こうやって分割すれば、地面についている部分と空中に浮いている部分を別々に考えることができそうだね!!
のた:そうだよ~。
そしてもう一点!今回は、ヒモに働く浮力を無視して考える。
空気の密度はヒモの密度に比べて一般的にかなり小さいと考えられるよね。てことは、ヒモに働く浮力は重力よりもかなり小さいはずだ。
だから、単純化のためにヒモに働く浮力を無視することにするよ。
黒豆:なるほど~。無視できるところは無視した方が議論が分かりやすくなりそうだよね。
- 風船の変わりに「手で」ヒモを支えるとして考える
- ヒモを微小部分に分割して考える
- ヒモに働く浮力は無視する
検討①:ヒモの浮いている部分に働く力は?
まずはヒモの浮いている部分に働く力から考えるよ。
ヒモの各微小部分の質量は\(m\)であるとしよう。
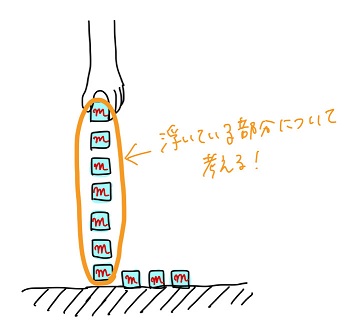
以下の図はヒモの浮いている部分のうち一番下の微小部分に働く力を示している。
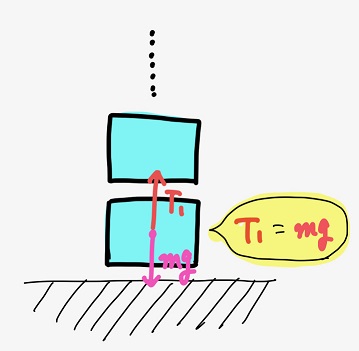
この一番下の微小部分では、下向きの力である重力\(mg\)と上向きの力である一つ上の微小部分からの張力\(T_{1}\)がつり合っているんだね。力のつり合いを考えると、張力は\(mg\)となるね。
黒豆:うん、そうだね。張力と重力が等しくなるんだね。
のた:では次に、一番下から二番目の微小部分に働く力を考えよう。
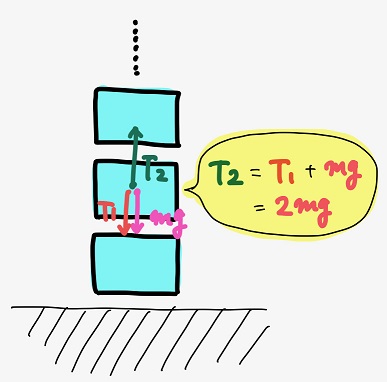
この微小部分には重力\(mg\)の他に、一つ下の微小部分からの張力\(T_{1}\)(\(mg\))と一つ上の微小部分からの張力\(T_{2}\)が働くね。
力のつり合いを考えると、\(T_{2}=2mg\)となることが分かる。
黒豆:おっ、張力が2倍になったねー。
さあ、そしてこのように空中に浮いている微小部分に働く力を順に考えていくと・・・。
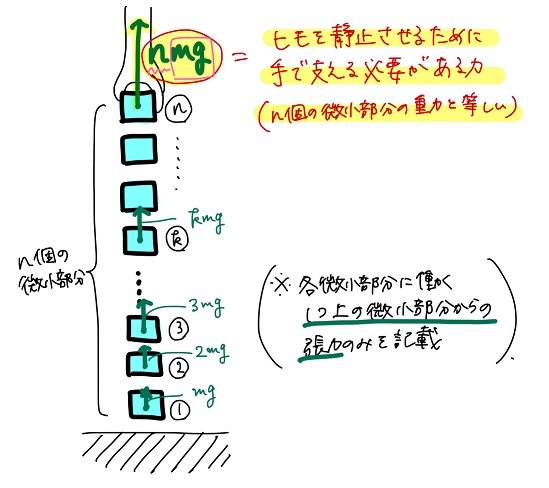
浮いている微小部分が\(n\)個存在する場合、
「手で支える力 = \(n\,mg\)」
となるんだ!
黒豆:そっか!下から\(k\)番目の微小部分に働く上向きの張力の大きさは\(k\,mg\)になるから、全部で\(n\)個の微小部分が浮いているとすると最終的に手が加える張力は\(n\,mg\)になって、\(n\)個分の微小部分の重力と等しくなるってことだね!!
のた:そういうこと!今日は冴えてるじゃん!!
黒豆:いつもは冴えてなくて悪いね~!!まあ事実だけどさ・・・。
検討②:ヒモの地面についている部分に働く力は?
のた:次に、ヒモの地面についている部分に働く力を考えよう。
ある微小部分に働く力は次のようになる。
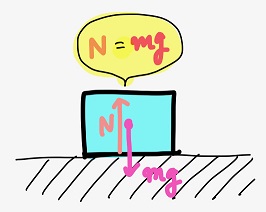
黒豆:重力\(mg\)と垂直抗力\(N\)がつり合う・・・。まあ、そうなるよね。
のた:そしてこれら、地面についている微小部分ももちろん静止している。横方向に動いたりしない。
つまり、これらに働く横方向の力は0(又はつり合っている)のはずだね。
結論:手が支えているのは・・・
のた:さあ、これまで検討してきた内容を一つの図にまとめてみよう。
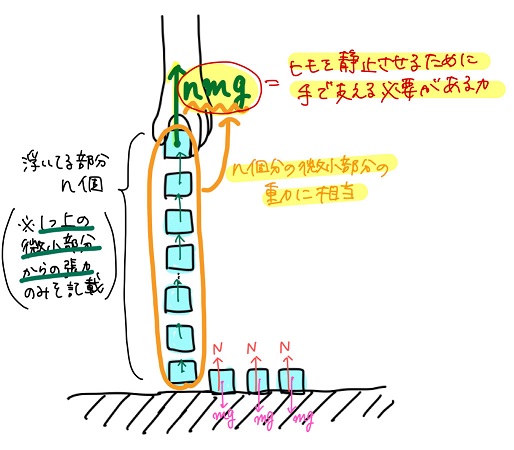
これを見て分かることはない??
黒豆:ええと・・・、
手で支えているのは浮いている部分のヒモだけで、地面についている部分のヒモには手からの力は及んでいない
ってことかな?
のた:そう、その通り!!
手で支える力はあくまでもヒモの浮いている部分だけに作用する
んだ!
地面についている微小部分は、手じゃなくて地面に支えられてるってことだね。
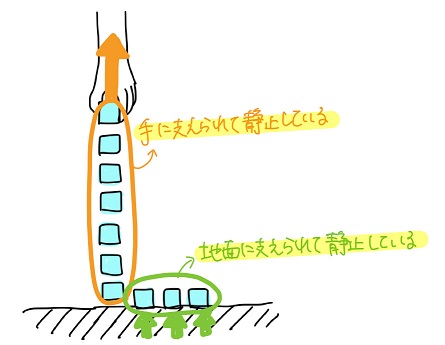
手を風船に置き換えて考えてても同じだ。
「風船+ヒモ」が静止している際の力のつり合いは、「風船」と「ヒモの浮いている部分」についてのみ考えればよい
ってことだね!
手で支える場合と風船が付いている場合とを比較してみたよ。
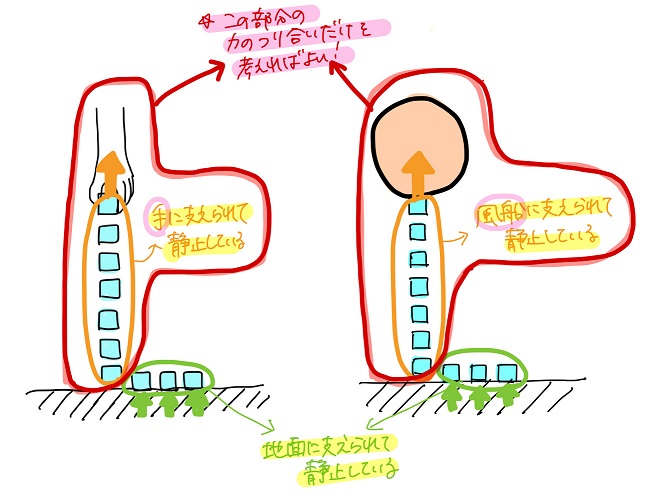
黒豆:ヒモの地面についている部分に働く重力に関しては風船との力のつり合いを考える必要がないんだね!
のた:そうだよ。これが面白いポイントだ!
実例:風船が上昇した場合について考えよう
のた:さっきの検討結果から、
「風船+ヒモ」が静止している際の力のつり合いは、「風船」と「ヒモの浮いている部分」についてのみ考えればよい
ってことが分かったね。
じゃあこの検討結果を元に、風船が上昇した場合に「風船+ヒモ」全体の力のつり合いをどう考えたらよいかを検討してみよう!
黒豆:風船が上昇したってことは、ヒモの浮いている部分の長さが増加したってことだよね。
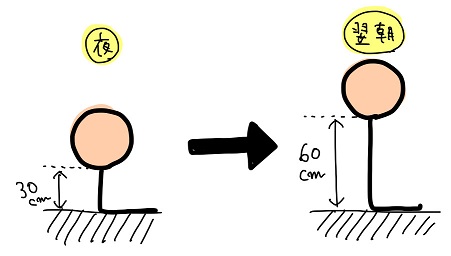
のた:そうだね。例えば以下のように、ある日の夜に浮いているヒモの長さが30cmだったものが翌朝見たら長さ60cmになっていたような状況だね。
のた:この状況における、「風船+ヒモの浮いている部分」全体に働く力の変化を示した図が以下だ。
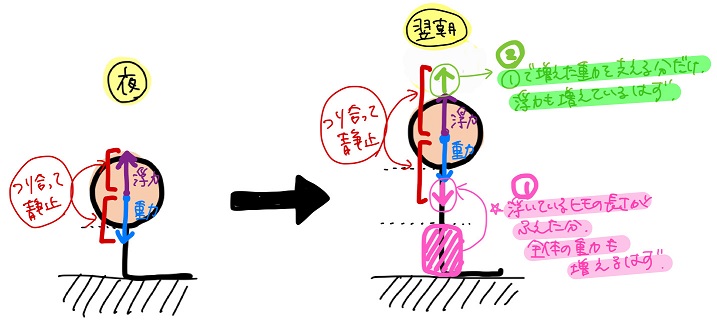
のた:ヒモの浮いている部分の長さが増加したってことは、その分だけ「風船+ヒモ」全体のつり合いにおける重力部分が増えたってことだ(図中①)。
黒豆:さっき検討した結論から考えると確かにそうなるよね!
のた:そして、その増えた重力分を支えるだけ風船自体の浮力も増えてるはずだ(図中②)。
そうしないと、風船がいくらか上昇した状態で再び静止するという状態は起こり得ないからね。
黒豆:うーん、まあそうなんだろうけど・・・。風船の浮力はどうやって増えたわけ?
のた:それはいろんな可能性があるなぁ。前回検討したように部屋の温度が変化したとか、部屋の空気の密度が変化したとか・・・。
まあ、本当はそこを考えるのが面白いところなんだけど、深入りすると大変だから今回はこの辺りでやめとこうか。
あくまでも今回は「静止した状態」について考えている訳だから、ヒモの浮いている部分の長さが増加したってことは風船に働く浮力も増加していないと力のつり合い的に辻褄が合わない、ってことだね。
まとめ
黒豆:ヒモ付きの風船のヒモの一部が地面についている状況なんてこれまで散々見てきたけど、力がどうつり合ってるかなんて考えたことがなかったなぁ。
ヒモの地面についている部分は風船との力のつり合いを考えなくていいなんて、びっくりしたよ~。
のた:そうでしょ~。
黒豆:そしてヒモを微小部分に分けて考えるなんて、目から鱗だよ~。
のた:微小部分に分けて考えるっていうのは、実は常套手段だったりするんだけどね。
黒豆:今回のヒモみたいに、一続きのものの各部分に異なる力が働いてそうな場合はそれを微小部分に分けて考えればいいんだね!
のた:そうだね。そうすれば新しい知見が得られるかもしれないよ!
黒豆:なんだか楽しそう!今度やってみよ~!!