滑車に働く力の正体
滑車と張力①
滑車に働く糸の張力を考える下準備として、そもそも「糸の張力とは”どういった力”なのか」について考察した。
糸の微小要素と滑車
の:さて立ち返って、今回考えたいことは、最終的には「滑車が糸から受ける力は何か?」という命題だね?前回見た「糸の微小要素と張力」の話をこの滑車を含んだ系で考えてみよう。

黒:これってどこの図?てか何?なんかバームクーヘンみたいだけど・・・笑
の:いやいや、これは滑車とヒモが接してる部分の拡大図だよ。ちなみに全体図はこちらね。
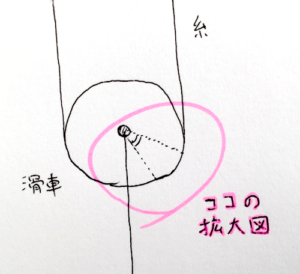
黒:なるほどなるほど。ちなみに糸がものすごく太くて違和感ありまくりなんだけど。
の:まあまあそれは気にしない。この方が説明しやすいからね。
の:滑車の車輪部分は円形なので、微小部分に取り出して考えると、微小角度 \(\Delta\theta\) の中心角を持つ円弧に糸の微小要素が沿っている形になる。そのため、糸の両端にかかる張力は微小角度 \(\Delta\theta\) の分だけ力のかかる向きがズレた力であるはず。さらに、微小要素は滑車の円弧と離れ無いので、そこには滑車からの抗力が働いていると考えられる。まとめると、以下の図の微小要素②に働く力は…
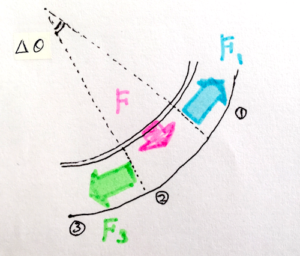
\(\boldsymbol{F}_{1}\):隣接する微小要素①から受ける張力
\(\boldsymbol{F}_{3}\):隣接する微小要素③から受ける張力
\(\boldsymbol{F}\):滑車から受ける垂直抗力
の:…と、それぞれの力に関して上記の様に書き記すことができる。
滑車にかかる力の正体
の:ここまで「糸」に注目して糸にかかる力を中心に考えを整理してきた。ここから、「滑車」に注目して考えていこう!
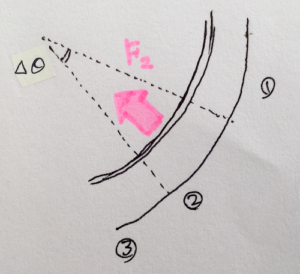
の:先ほどは糸の微小要素を中心に、これにかかる力を記述した。対して、今回の図では「糸の微小要素が滑車に与える抗力」を記している。つまり先の微小要素が滑車から受ける垂直抗力 “\(\boldsymbol{F}\)” の反作用の力に相当する。この力が「滑車に接する各微小要素」からそれぞれ滑車に作用するので、下の図のように描ける。
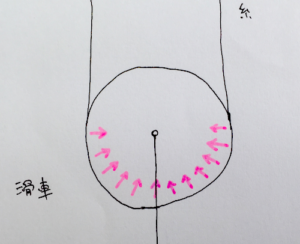
の:この微小要素から受ける力の合力こそが「動滑車が糸から受ける力」に他ならない。つまり、動滑車に働く力は直接的に「糸の張力」が働くわけではなく、「糸が滑車の円弧に掛かることで、糸の微小要素の両端にかかる張力に角度差が生じて打ち消し合わず、それらによって滑車と糸の微小要素との間で抗力が発生し、それぞれの糸の微小要素から生じた抗力の滑車への合力」と言える。(息が切れる。)
黒:じゃあ、滑車に働く力はこの「微小要素から受ける力の合力」が滑車の両端の糸2つに分けて描かれていたってこと?
の:その通り!実際にはあくまで”合力”なのでどう描くのが良いのか悩ましいところだよね。力が生じている力点は滑車と糸が接してる面全体なので、イメージ的には…こんな感じかなぁ。

黒豆さんへの宿題
具体的に各微小要素からの抗力の合力を計算してみよう!