黒豆:ああ~。それにしても、\(\sin x\)のグラフの描き方の話は衝撃的だったよー。今までなんて適当にグラフを描いてたんだろう・・・って感じ。さすがに反省したよ・・・。
↓\(\sin x\)のグラフの描き方に関する記事はこちら!!↓
のた:お役に立てたならよかった~。
黒豆:うん。すごく役に立った!!\(\sin x\)とか\(\cos x\)とかのグラフが正確に描けるようになったし!もっといろんなグラフの描き方も考えてみたいな~。
のた:ふーむ、よし。じゃあ、前回題材にした\(\sin x\)のグラフを利用して、より複雑なグラフを描いてみようか!
\(\sin x\)が含まれるグラフ、例えば\(y=x \sin x\)とか\(y=x^2 \sin x\)とかのグラフを描いてみよう。
黒豆:おー、面白そう!
のた:そしてせっかくだから、今回は
「微分を使わずにグラフの概形を予測する」
という面白い方法に挑戦してみようか!
黒豆:へっ?どういうこと??前回の方法と何か違うの?
微分せずにグラフの概形を予測してみよう!
微分しないって、つまりどういうこと??
のた:つまりね、
「関数全体を微分して極大点や極小点、変曲点を求めるという面倒な過程を飛ばして、グラフの概形をある程度程度予測してみる」
ってことだよ!
黒豆:えっ?そんなことできるの?グラフって微分しないと描けないと思ってたけど・・・。
のた:正確性を求める場合はもちろん微分するのが一番だけど、微分しなくても概形を予測できる場合もあるんだよ。
例えば、今回は以下のような\(\sin x\)を含む関数を考えるんだったよね。
\(y=x \sin x\)
この関数は\(y=x\)と\(y=\sin x\)という2つの関数の積だ。
ということは、もし\(y=x\)と\(y=\sin x\)のグラフの形が微分により(微分するまでもないかもだけど)正確に分かっているなら、\(y=x \sin x\)のグラフの形はわざわざ微分しなくてもある程度予測できると思わない?

黒豆:ああ~、確かになんか描けそうな気がせんでもない・・・。
のた:こんな風に、
「基本的な関数のグラフの形が正確に分かっていれば、それらの関数の積や和のグラフの概形をある程度予測することができる」
ことが多いんだ。
黒豆:なるほどぉ。基本的な関数の形を利用してより複雑な関数の形を予測するんだね!
のた:その通り!!
グラフの概形を予測することのメリットは?
のた:グラフを正確に描くには確かに微分が必要だ。
でも、グラフをどこまで正確に描く必要があるかは状況に応じて異なるよね。
例えば問題によっては、グラフの形がそこまで正確に分からなくても、\(x>0\)だとか\(x\)が単調増加しているとかその程度の情報が分かればよい場合もある。
こういう場合にわざわざ微分までするのは、手間がかかるだけで正直無駄だ。微分って大変だしね。
黒豆:つまり、グラフの概形だけ分かればいいって場合に余計な手間をかけないために、概形を予測する方法を使うといいってことだね。
のた:そうそう。まあ、グラフを正確に描く必要がある場合であっても、最初にグラフの概形を大まかに予測してから微分する方が効率がよいこともあるしね。
黒豆:なるほど~。確かに、森を見てから木を見る方がよいこともありそうだよね。
実例:\(y=x \sin x\)のグラフの概形を予測してみよう
のた:じゃあ、早速実際にやってみようか。
\(y=x \sin x\)について、とりあえず1周期分(\(x=0~2π\))のグラフを描くことにする。これ以降は\(0≦x≦2π\)という前提で議論するよ。
\(y=x \sin x\)について考えるときには、基本となる\(y=x\)と\(y=\sin x\)のグラフを参考にするんだったね。
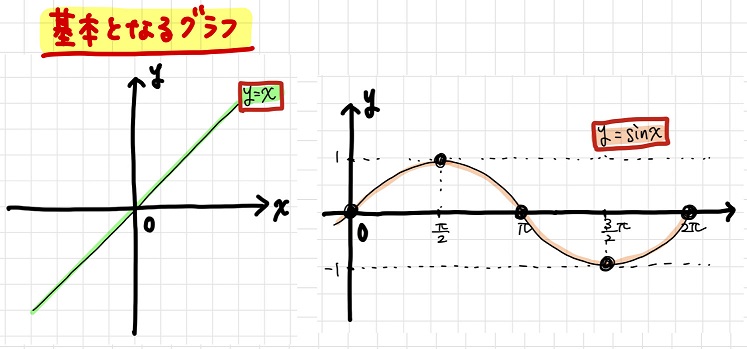
\(y=\sin x\)のグラフからヒントを得る
まずは\(y=\sin x\)のグラフを見てみよう。ここから\(y=x \sin x\)のグラフを描く上でのヒントが見つからないか考える。
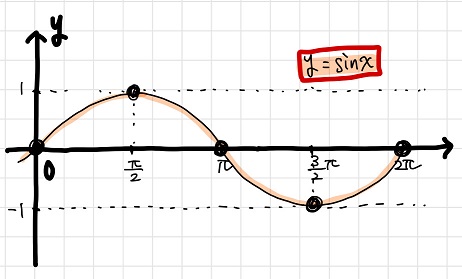
黒豆:ヒント?一体どう考えればいいの??
のた:例えば、\(y=\sin x\)のグラフの特徴って何?
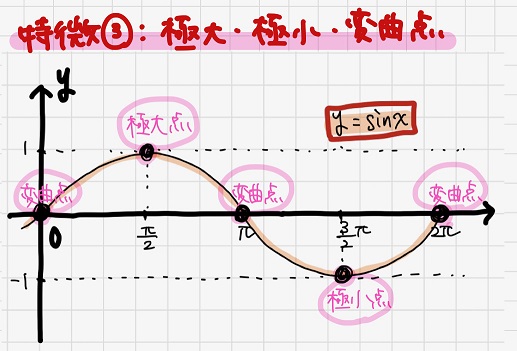
黒豆:特徴かぁ・・・。ざっと思いつくのはこんな感じかなあ。
①\(-1≦\sin x≦1\)
②周期は\(2π\)
③\(x=0,π,2π\)で変曲点、\(x= \frac{π}{2}\)で極大点、\(x= \frac{3}{2}π\)で極小点をとる
のた:うん、大体こんな感じだよね。じゃあこの①~③の特徴について順に検討してみようか!
「\(y=\sin x\)のグラフの特徴①:\(-1≦\sin x≦1\)」から考える
まず特徴①について。
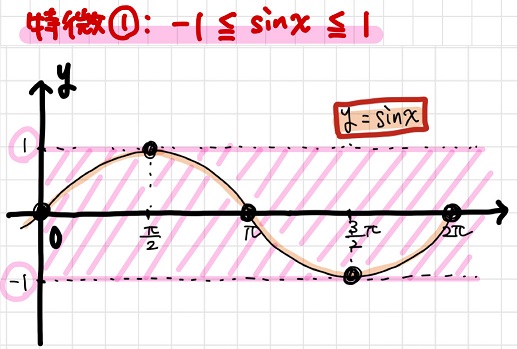
\(-1≦\sin x≦1\)ってことは、\(-x≦x \sin x≦x\)ってことだ。これってつまり、
\(y=x \sin x\)のグラフは必ず\(y=-x\)と\(y=x\)のグラフの間にある
ってことだよね。
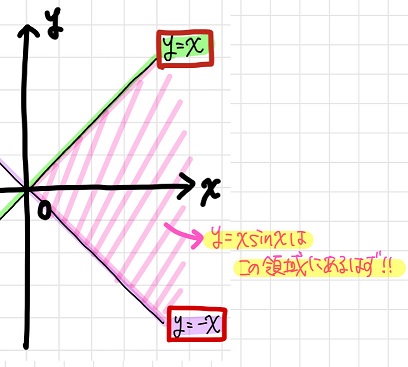
黒豆:おお!確かにそうなるね!!
のた:さらに言えば、\(y=x \sin x\)は
\(\sin x=1\)のときには\(y=x\)になり、
\(\sin x=-1\)のときには\(y=-x\)になる。
つまり、
\(\sin x=1\)のとき\(y=x \sin x\)は\(y=x\)上の点を通り、
\(\sin x=-1\)のとき\(y=x \sin x\)は\(y=-x\)上の点を通る
ってことが分かる。
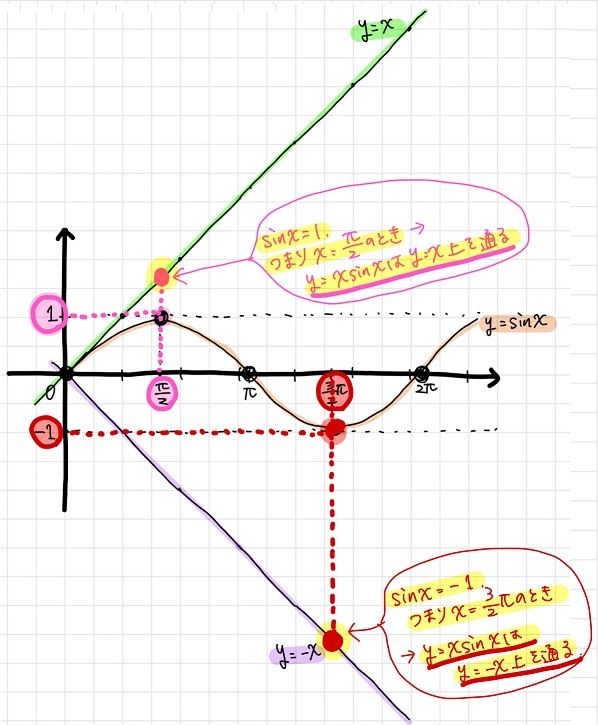
黒豆:おお、なるほど!!
- \(y=x \sin x\)のグラフは必ず\(y=-x\)と\(y=x\)のグラフの間にある
- \(\sin x\)=1のとき\(y=x \sin x\)は\(y=x\)上の点を通る
- \(\sin x\)=-1のとき\(y=x \sin x\)は\(y=-x\)上の点を通る
「\(y=\sin x\)のグラフの特徴②:周期は\(2π\)」から考える
のた:次に特徴②について検討しよう。特徴②は、\(y=\sin x\)の周期が\(2π\)だって話だったね。
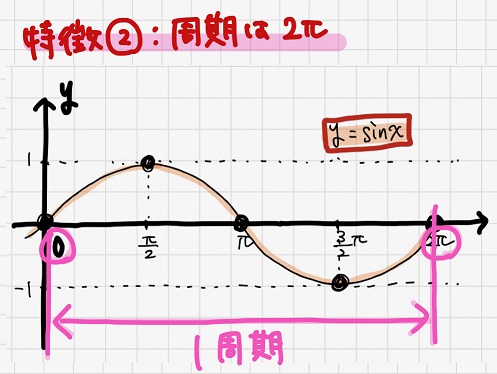
\(y=x\)のグラフには周期がない(単調増加するだけ)けど、\(y=\sin x\)のグラフには周期がある(つまり振動する)。
てことは、これらの積である\(y=x \sin x\)のグラフも\(y=\sin x\)と同じく周期\(2π\)で振動するってことだ。
黒豆:え?そうなの??今のところよく分からなかった。
のた:\(y=\sin x\)に周期があるってことは、\(y=\sin x\)のグラフは周期的にx軸を通過するってことでしょ?つまり、周期的に\(y=0\)になるってことだよね。
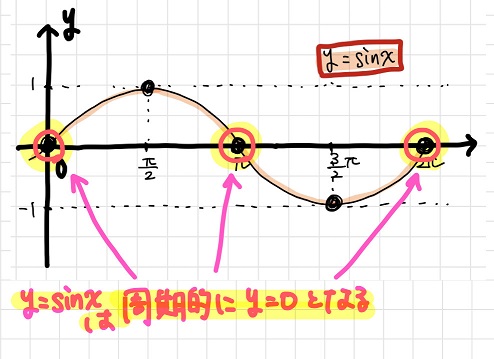
\(y=\sin x\)のグラフがx軸を通過するときには、\(y=x \sin x\)のグラフも\(x\)軸を通過するはずだ。\(\sin x\)=0なら\(x \sin x\)=0になるからね。
つまり、\(y=\sin x\)と\(y=x \sin x\)は同じタイミングで\(x\)軸を通過する=周期が同じ、ってことになるんだよ。
黒豆:なるほど、そっか!!
- \(y=x \sin x\)のグラフの周期は、\(y=\sin x\)と同じく\(2π\)である
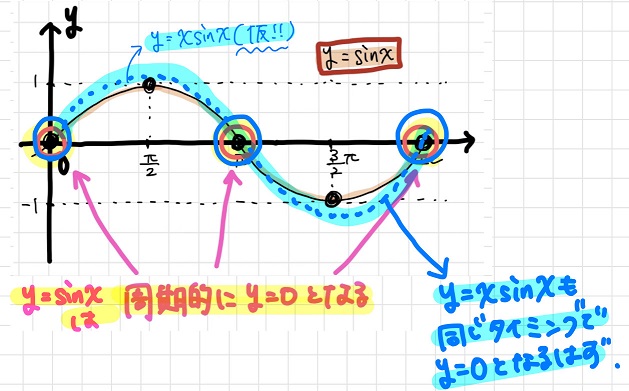
一旦グラフの概形を描いてみよう
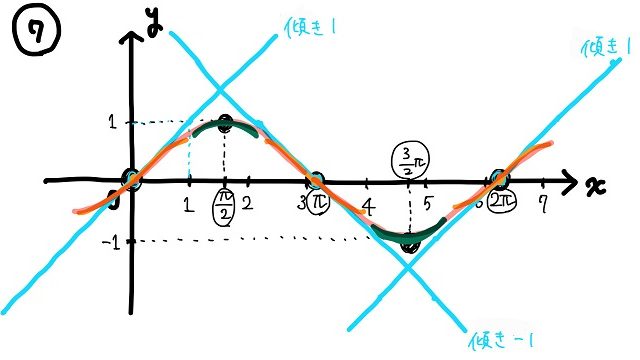
のた:とりあえずこれまで考察した内容を盛り込むと、\(y=x \sin x\)のグラフは以下のような形になりそうだね。
黒豆:おお、なんとなくグラフのイメージが沸いてきたね~。
のた:そうでしょ?グラフの概形を掴むだけならこれくらいで十分だと思うよ。
「\(y=\sin x\)のグラフの特徴③:変曲点・極大点・極小点の位置」から考える
のた:次は特徴③だね。特徴③は、\(y=\sin x\)の極大点・極小点・変曲点の位置に関する話だった。
特徴②で検討したように、\(y=\sin x\)と\(y=x \sin x\)の周期は同じ\(2π\)だ。だから、\(y=x \sin x\)の場合も\(0≦x≦2π\)の間に極大点と極小点があるはずだね。
さて、果たして\(y=\sin x\)と\(y=x \sin x\)の極大点・極小点は同じなのかな??
黒豆:うーん、この概形を見る感じだと少しずれてる気がするけど・・・。
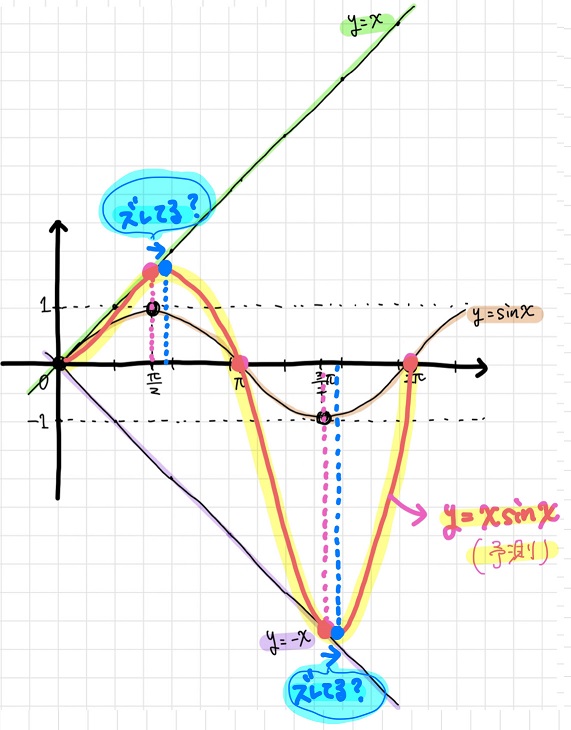
のた:そう。実は、
\(y=x \sin x\)の極大点と極小点は、\(y=\sin x\)の極大点・極小点よりもx軸の正の方向に少しずれた位置にある
んだ!
例えば極大点について考えてみよう。
\(y=x \sin x\)のグラフは\(x= \frac{π}{2}\)のときに\(y=x\)上の点を通り、\(x=π\)のときに\(y=0\)を通るんだったね。
この2点を通り、\(y=x\)のグラフより下の範囲で\(0≦x≦2π\)で上に凸になるためには、
極大点はどうしても\(x= \frac{π}{2}\)より少し\(x\)軸の正の方向にならざるを得ないんだ。
だって、もし\(y=\sin x\)と同じく\(x= \frac{π}{2}\)のときに\(y=x \sin x\)が極大となるとしたら、\(y=x \sin x\)のグラフの一部が\(y=x\)のグラフより上に出ちゃうからね。
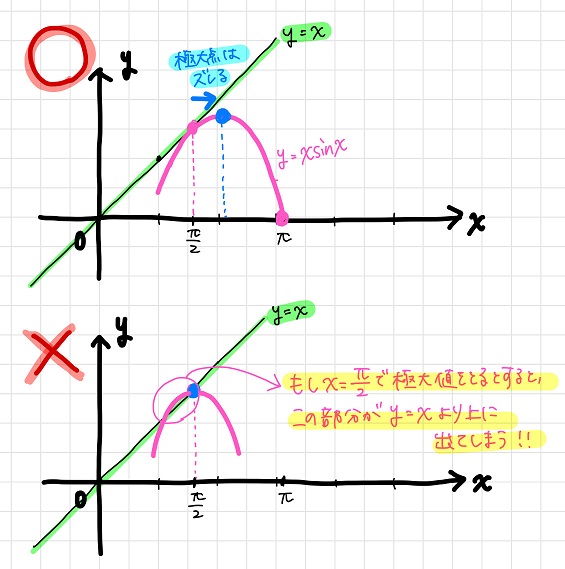
黒豆:おお、確かに・・・!!こういう細かいことも予測できちゃうんだね。
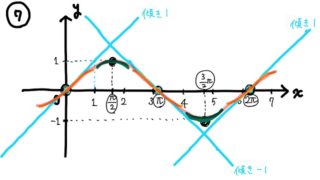
\(y=x \sin x\)のグラフの最終的な概形はこうなる!!
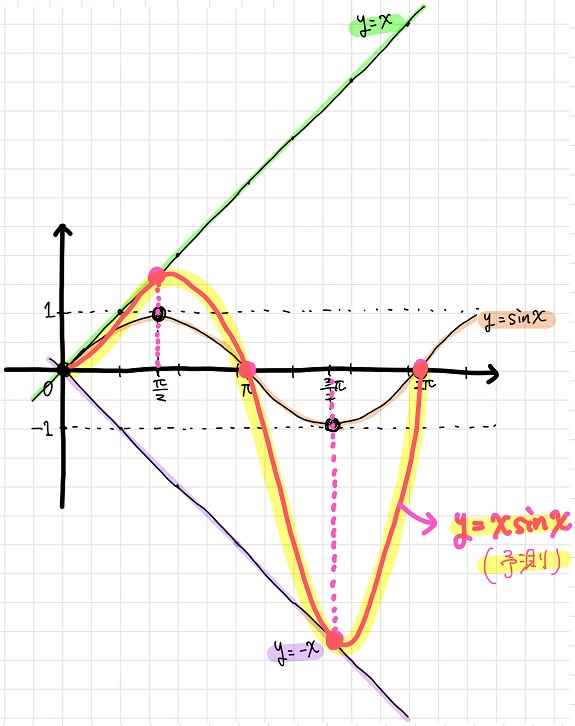
のた:さあ、これまでの情報を全て合わせると、\(y=x \sin x\)のグラフの概形は\(0≦x≦2π\)の範囲で以下のようになると考えられるね。

黒豆:\(y=x\)と\(y=-x\)のグラフの間を\(\sin x\)と同じ\(2π\)周期で振動しているようなグラフになるんだね~。
のた:そうだね。ちなみに\(0≦x≦2π\)以外の範囲のグラフの形も簡単に予測できるよ。
\(y=x \sin x\)は\(y=x\)と\(y=\sin x\)という奇関数(原点に対して点対称な関数)同士の積だよね。
つまり\(y=x \sin x\)は偶関数(y軸に対して線対象な関数)になる。
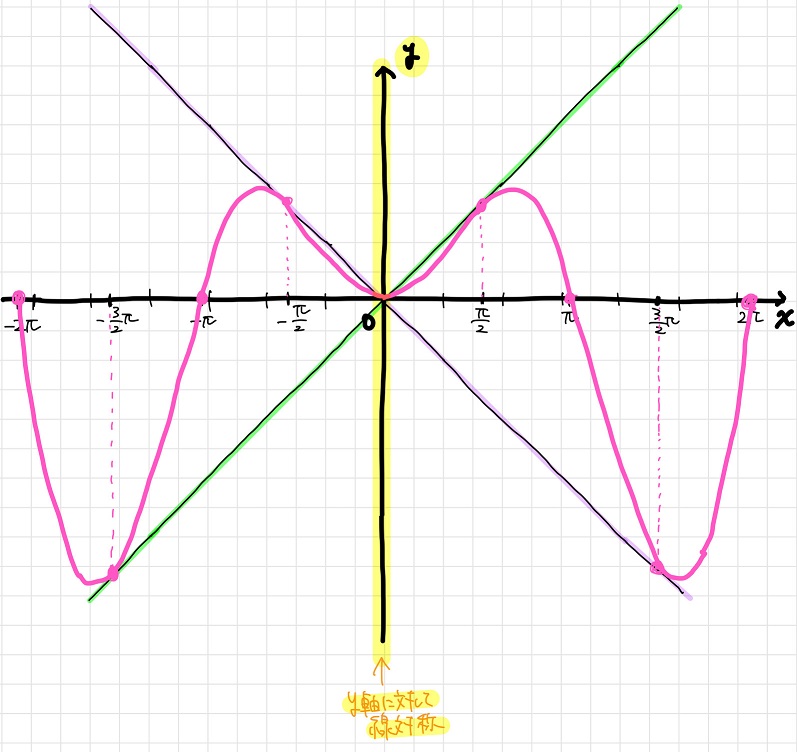
さらに、\(y=x \sin x\)のグラフの周期は\(2π\)で変わらないけど、\(y=x\)と\(y=-x\)のグラフは原点から離れるにつれて上下方向に広がるよね。
てことは、\(y=x \sin x\)のグラフは原点から離れるに従ってよりシャープな形で振動するはずだ。こんなイメージだね。
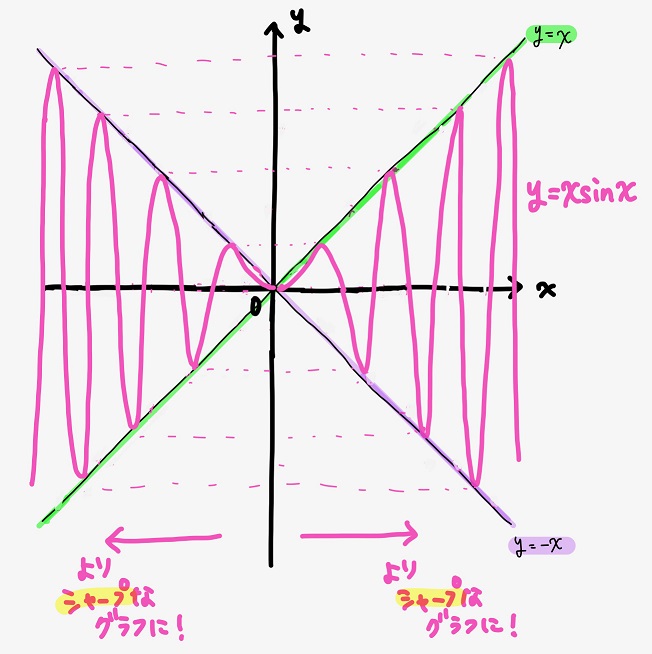
黒豆:おお~!!ここまで描けば、\(y=x \sin x\)の全体像がよく分かるね!
のた:そうだね。ここまで描いた上で、細かい部分、例えば\(0≦x≦π/2\)部分がどうカーブしているのかなどを知りたい場合は微分してみるといいね。
最後に、これまで出てきた全グラフ(\(y=x\)、\(y=-x\)、\(y=\sin x\)、\(y=x \sin x\))をグラフ描画サービスで正確に描画してみたよ。

(GraphSketchにて描画)
黒豆:お~、予測した通りの形になってるね!!
実例:\(y=x^2 \sin x\)のグラフも同じように予測できる!
のた:\(y=x^2 \sin x\)のグラフの概形も\(y=x \sin x\)と同じように予測することが可能だよ。予測結果はこんな感じになるね。
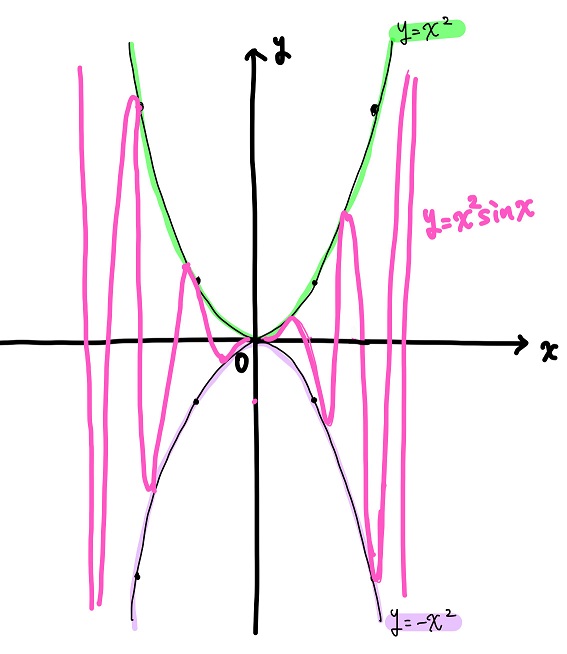
黒豆:そうだよね、\(y=x \sin x\)の場合の\(y=x\)が\(y=x^2\)に置き換わっただけだから、\(y=x^2\)と\(y=-x^2\)の間を周期\(2π\)で振動してるグラフってことになるんだね。
のた:そうだね。違いと言えば、\(y=x^2\)が偶関数だから、\(y=x^2 \sin x\)は偶関数と奇関数の積で奇関数になるってことくらいかな。
黒豆:あ、そっか!だから\(y=x^2 \sin x\)のグラフは原点に対して対象になってるんだね!
のた:そゆこと!
一般化:\(y=f(x) \sin x\)のグラフはどれも同じように予測できる!
のた:これまで\(y=x \sin x\)や\(y=x^2 \sin x\)のグラフの概形について考察してきたけど、実は
\(y=f(x) \sin x\)のグラフの概形はどれも同じように予測することができる
んだ。
黒豆:一般化が可能ってことだね!
のた:その通り!
具体的には以下の手順で描くことができるよ。
- \(y=f(x)\)、\(y=-f(x)\)のグラフを描く
- \(y=f(x)\)、\(y=-f(x)\)のグラフ間の領域、\(0≦x≦2π\)の範囲に\(y=\sin x\)のグラフを伸縮させながら描く
- 手順2のグラフを\(0≦x≦2π\)以外の範囲に拡張する。
※手順3において、
\(y=f(x) \sin x\)が偶関数の場合:グラフが\(y\)軸に対して線対称になるように描画
\(y=f(x) \sin x\)が奇関数の場合:グラフが原点に対して点対称になるように描画
黒豆:\(y=x \sin x\)のグラフの予測過程を一度自分で考えた後だから、上の手順も納得できるね~!
のた:そうでしょ。まず最初に自分で具体例を考えてみてから、それを一般化できるか考える方が頭に残るよね。
まとめ
のた:今回は\(y=f(x) \sin x\)の場合について説明したけど、他の場合でも
「基本的な関数のグラフの形が正確に分かっていれば、それらの関数の積や和のグラフの概形をある程度予測することができる」
ことはあるよ。
色々な関数に関して、どこまでグラフの概形を予測することができるか自分で試してみるのも面白いね。
黒豆:そうすればグラフの扱いに慣れることができそうだね!よし、早速修行だ~!!
のた:自分で試行錯誤するのが上達への道だよ!がんばって~!!