黒豆:(・・・ゴリゴリゴリ)
のた:ん?何やってるの??
黒豆:ちょっと数学の問題を解いてるんだ~。といっても、簡単な三角関数の練習問題だけどね。
のた:ほう。どれどれ??
黒豆:今sin\(x\)のグラフが描けたとこだよ~。
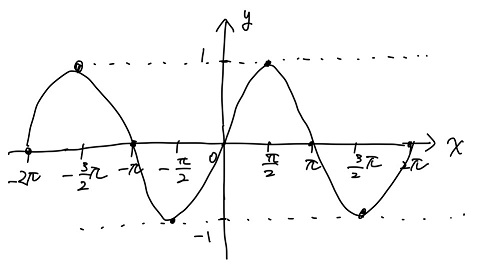
のた:・・・ほう。なるほど。。。黒豆。これじゃあsin\(x\)のグラフを描いたなんてとても言えないなぁ。
黒豆:えええっ!???何で??どこからどう見たってsin\(x\)のグラフじゃん!!
のた:うーん、まあ間違ってるわけではないんだけどねぇ・・・。
そうだ、ちょうどいい機会だから、グラフの描き方について考えてみようか!
グラフの描き方ひとつで問題が解けるかどうかも変わってくるんだよ。
黒豆:・・・はあ~い。
黒豆が描いたグラフの問題点とは??不正確なグラフの特徴!
黒豆:(何で別に間違ってるわけでもないのに説教されなきゃいけないんだよ~。)ぶつぶつぶつ・・・。
のた:・・・なんか不服そうだねぇ。じゃあとりあえず、黒豆が描いたグラフの問題点について考えてみようか。

黒豆:別に普通のsin\(x\)のグラフだとおもうけどお~??
のた:ほう、自信満々だねぇ。
じゃあまず、黒豆が描いたグラフの縦軸と横軸の比率について見てみよう。
黒豆のグラフだと、\(y\)軸上の1と\(x\)軸上の\(π\)がそれぞれ原点から同じくらいの位置にあるように見える。
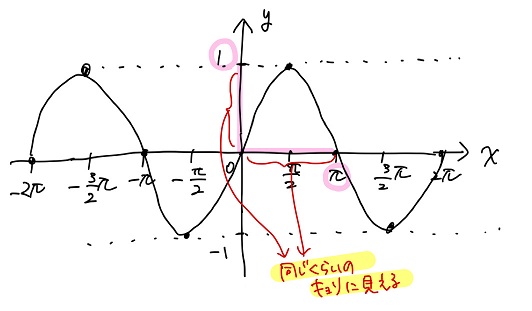
\(π\)の具体的な値はいくつだっけ?
黒豆:確か・・・3.14だよね。
のた:そうだ。てことは、黒豆のグラフだと\(y\)軸上の1と\(x\)軸上の3が同じくらいの位置にあることになる。
これって\(y\)軸と\(x\)軸の比率が違ってる、ってことだよね。\(x\)軸上のメモリが大分詰まっちゃってる。
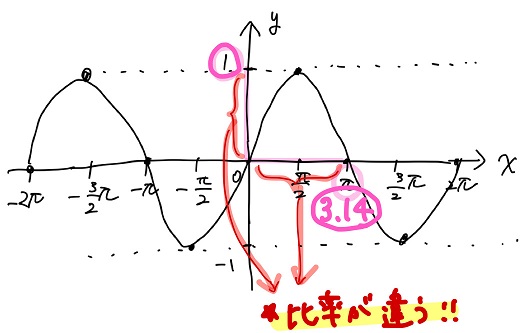
黒豆:たっ、確かに・・・!!
のた:まずこれが、第一の問題点だね。
黒豆:ぐぬぅ。
のた:問題点はまだある。
sin\(x\)を微分するとcos\(x\)になるよね。つまり、sin\(x\)のグラフの接線の傾きはcos\(x\)になるはずなんだ。
例えば、\(x\)=0のときの場合を考えてみよう。
cos0=1だから、\(x\)=0のときにはsin\(x\)のグラフの接線の傾きは1になるはずだよね。
つまり、本来ならこうなるはず。
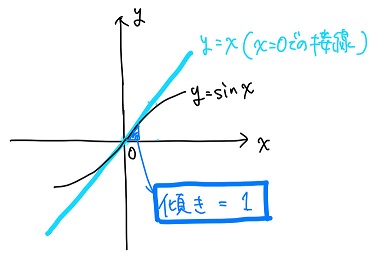
でも黒豆のグラフだと、\(x\)=0での接線の傾きは・・・。大体0.5~0.6くらいかなぁ。少なくとも1にはなっていないよね。
というかそもそも、\(x\)軸と\(y\)軸の比率が違うから傾きを考えるのもやりにくいし。
黒豆:ぐおおおお・・・。
のた:ざっと見た感じだとそんなところかなぁ。一言で言うと黒豆のグラフは、
「通る点を適当にとってそれっぽい形につなげただけ」
ってことだね。
黒豆:ぐはああ!!!かっ・・・、完敗です・・・。
のた:何で不正確なグラフだって言ったか、これで分かったでしょ?(笑)
黒豆:はい・・・。うぬぼれておりました・・・。
- \(x\)軸と\(y\)軸のメモリの比率が異なる
- グラフの傾きが不正確
のた:ふふふ。数学ではグラフを正確に描くことがすごく重要なんだよ。
グラフを正確に描けない場合、気付くべきことに気付けないこともあるんだ。
例えば、ある2つのグラフが本当は接している場合であっても、グラフの描き方ひとつでそれらのグラフが重なっていると早とちりしちゃったりね。
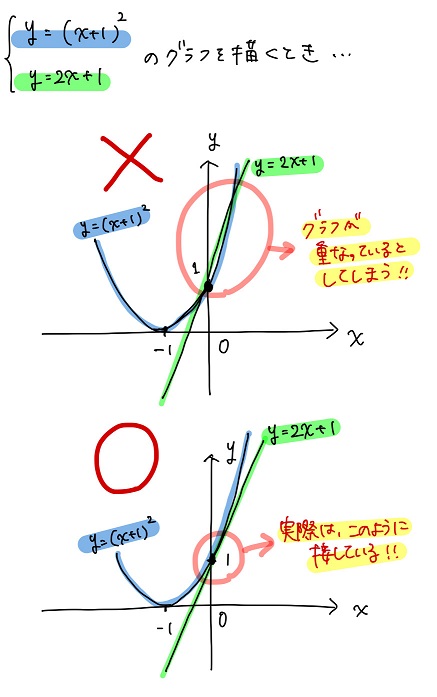
黒豆:うん。自分で描いたグラフを見て自分で勝手に勘違いしちゃうこと、確かに私もあるなぁ・・・。適当にグラフを描くといろいろな誤解をしやすくなるんだね。
のた:じゃあ次に、僕が実際にどうやってsin\(x\)のグラフを描いているかを説明しよう!
黒豆:はい!勉強させていただきますっ!!
sinxのグラフを正確に描いてみよう!!
①グラフを描く範囲を考える
のた:まず考えるのは、「グラフを描く範囲」だね。
普通sinxのグラフだったら1周期分、つまり0~2\(π\)までのグラフを描けば十分なことが多いけど、問題によっては2周期分、3周期分のグラフが必要なこともあるからね。
そして、描画が必要な範囲に基づいて\(x\)軸と\(y\)軸の範囲を決める。
今回はとりあえず、1周期分のグラフを描くことにして、それが描けるだけの範囲を確保する。
どのくらいの縮尺で描くかを考えれば、大体どのくらいの長さの軸を描けばいいかが分かるよね。
まあでも、ここは後から簡単に修正できるからそこまで神経質にならなくてもいいよ。
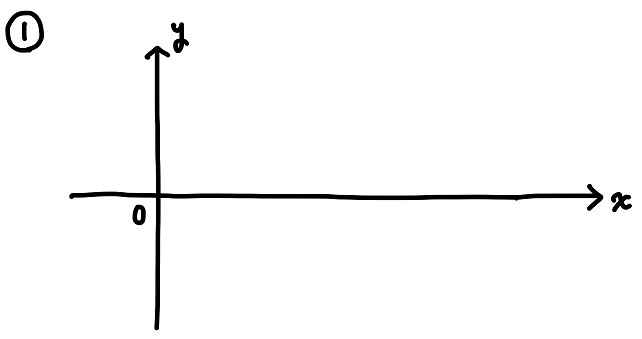
②軸上にメモリを振る
のた:次に、「軸上にメモリを振る」。
\(x\)軸と\(y\)軸の比率が同じになるように注意することが大切だね。
黒豆:はいぃ・・・。
のた:今回は1周期分、つまりx = 0~2\(π\)までの範囲のグラフを描くから、まず\(x\)軸上にその範囲のメモリを振ろう。
\(π\)=3.14だから、2\(π\)=6.28だよね。
つまり、\(x\)軸上に0~7までの整数のメモリを振れば1周期分のグラフが描けることになる。メモリが等間隔になるように気をつけて振ろう。
のた:で、sin\(x\)の最大値は1だから、\(y\)軸は1までのメモリをとれば十分だね。このとき、\(x\)軸上のメモリと比率が同じになるように気をつけよう。
黒豆:はいいぃ・・・。
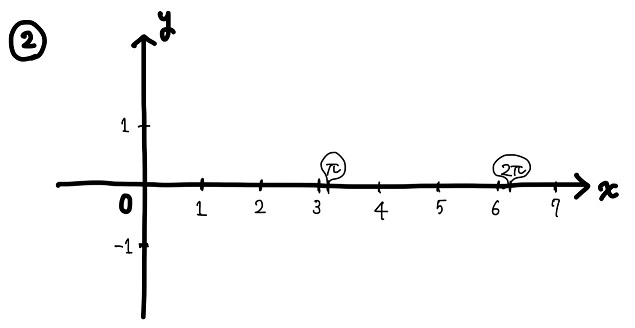
③必ず通ると分かっている点に大きく印をつける
のた:次に、「必ず通ると分かっている点に印をつける」。
極大、極小点や変曲点などの点に印をつけるんだ。この印がグラフを描画する上での基準となる。
sinxの場合だと、(0, 0)、(\(\frac{π}{2}\), 1)、(\(π\), 0)、(\(\frac{3}{2}\)\(π\), -1)、(2\(π\), 0)あたりかな。
このとき、分かりやすいようにできるだけ大きな印をつけておこう。僕はいつも大きな黒丸をつけてるよ。
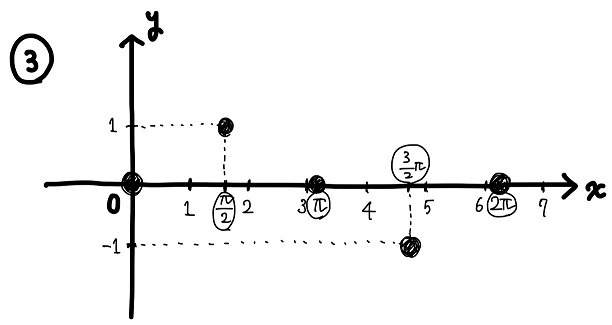
④主要な接線を引いておく
のた:ここはちょっとしたポイントだよ。
「先にグラフの接線を引いておく」
んだ。
接線を引くことでグラフの傾きを定めることができるから、より正確なグラフが描ける。
グラフを描くときに傾きまで意識している人は少ないかもしれないけど、ここをきちっとやっておくとグラフの正確性が驚くほど増加するんだ。
黒豆:うん、確かに傾きまで正確に意識したことはなかったなあ・・・。
のた:sinxの場合だと、とりあえずx軸上の点である(0, 0)、(\(π\), 0)、(2\(π\), 0))での接線を書き込んでおけばいいかな。
特に変曲点周りはグラフが描きづらいから、変曲点での接線は書き込んでおいた方がよいね。
冒頭でも書いたようにsin\(x\)のグラフの接線の傾きはcos\(x\)になるから、各点でのcos\(x\)の値を計算すれば接線の傾きが求まる。
計算の結果は次のようになる。
点(0, 0) → 接線の傾き:1
点(\(π\), 0) → 接線の傾き:-1
点(2\(π\), 0) → 接線の傾き:1
この結果を図に描き込んでおこう。
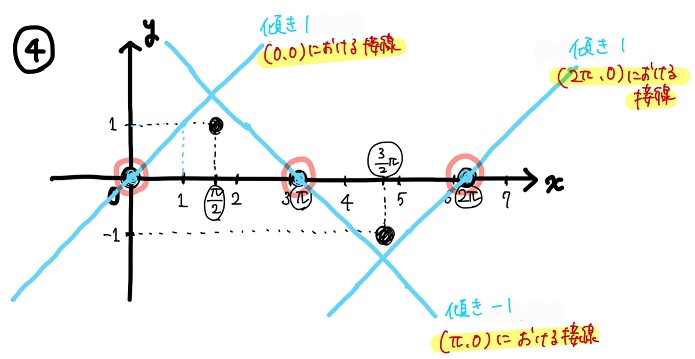
⑤変曲点周りのグラフの形を描き込む
のた:次に、④で引いた変曲点での接線を参考にして「変曲点周りのグラフを描画」しよう。
変曲点ではグラフの形が「上に凸⇔下に凸」に変化するからグラフを描くのが難しいんだけど、接線に沿うようにして描けば描きやすいよ。
こんな感じ。
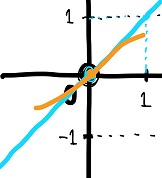
黒豆:おお~、確かに!なんか綺麗に描けてる気がする!!
のた:そうでしょそうでしょ。グラフ全体としてはこうなるよ。
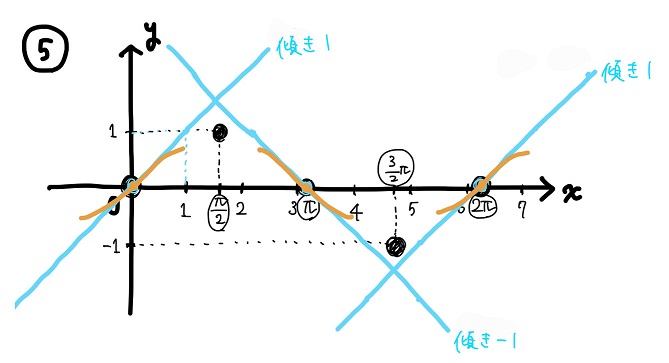
⑥極大・極小周りのグラフの形を描き込む
のた:最後に、「極大・極小値をとる点周りのグラフを描画」しよう。
sin\(x\)の場合、0~2\(π\)の範囲で極大・極小値をとる点は(\(\frac{π}{2}\), 1)と(\(\frac{3}{2}\)\(π\), -1)だね。
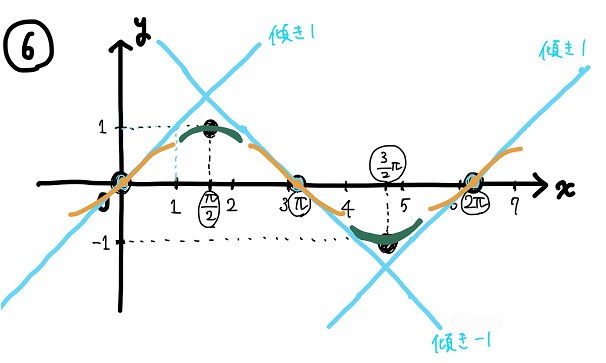
⑦グラフをつなぎ合わせて、完成!!
のた:最後に、「これまで描いたグラフをつなぎ合わせれば完成」だ!!
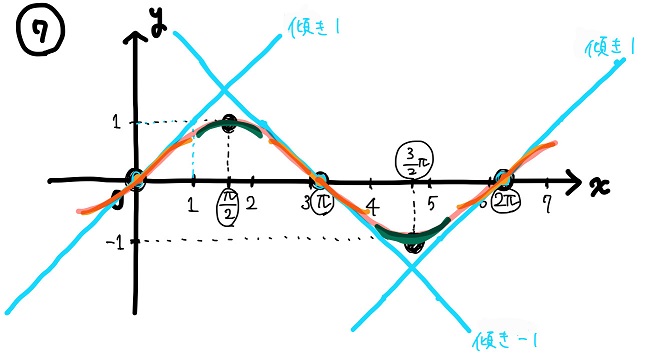
黒豆:おお~!!なんか綺麗なグラフになった気がする!!
のた:黒豆が最初に描いたグラフと比較してみよっか。
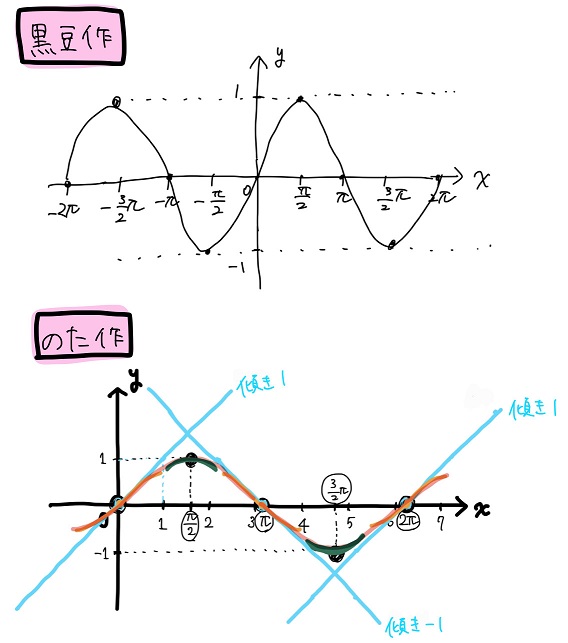
黒豆:ううぅ・・・。完敗です・・・。
- ①グラフを描く範囲を考える
- ②軸上にメモリを振る
- ③必ず通ると分かっている点に大きく印をつける
- ④主要な接線を引いておく
- ⑤変曲点周りのグラフの形を描き込む
- ⑥極大・極小周りのグラフの形を描き込む
グラフを正確に描くことのメリット
のた:正確にグラフを描くといいことがたくさんあるんだ。例えば以下のようなことだね。
- 問題を解く際の重要なポイントに気付くことができる(グラフ同士が接しているor接していないなど)
- グラフ内のある領域の面積を大凡予測することができる
要するに、
「問題の中の状況を正確にとらえることができる」
ってことだね。
ちなみに、数学が得意な人に図解がヘタな人はいないんだよ~。
黒豆:そっ、そうっすよね・・・。精進します・・・。
まとめ
黒豆:今まで自分がどれだけグラフを適当に描いてきたかがよく分かったよ・・・。というか、グラフを正確に描くことにそこまで重要性を感じていなかったという方が正しいのかも。
グラフを正確に描くって、大切なことなんだね~。
のた:その重要性が分かってもらえたなら十分だよ。グラフの描き方は訓練で上達させることができるから、これから意識していけばいいんだよ。
今回sinxのグラフを描く際になぞった手順を他のグラフを描く際にも応用しつつ、自分で試行錯誤しながら自分なりのグラフの描き方を確立していってね。
黒豆:はい、師匠!!がんばります!!!





